filmov
tv
Linear Algebra 10c: A Row Reduced Echelon Form (RREF) Challenge

Показать описание
Linear Algebra 10c: A Row Reduced Echelon Form (RREF) Challenge
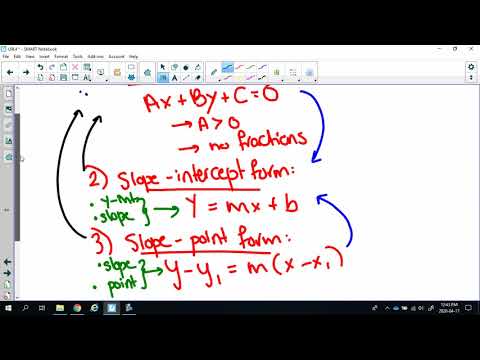
Math 10C General Form
Math 10C Solving Linear Systems Graphically
Math 10C: Slopes of Lines 1
Math 10C Equations of Linear Relations Lesson 1
10C - Lesson 4.1 - Slope of a Line
Math 10C Number of Solutions to a Linear System
Linear Equations - Algebra
Math 10C Unit 4B Equations of Linear Relations L5: Further Practice
U9L2 Math 10C
Linear Algebra 10a: Introduction to the Row Reduced Echelon Form (RREF) of a Matrix
Math 10C: Solving Systems of Equations Using Elimination 1
Solving Systems of Equations By Graphing
Math 10C: Solving Systems of Equations with Word Problems 1
Math 10C Systems of Linear Equations Lesson 1
Math 10C - 7.1 - Systems of Linear Equations
MATH 10C: Finding Slopes, Solving Linear Equations
Math 10C: An Introduction to Systems of Linear Equations
10C - 7.2 - Systems of Linear Equations
Solving Systems of Linear Equations By Graphing │Algebra
Solution to Problem 10C, Take home test 2, Intermediate Algebra
Math 10C - General Form of a Line
Math 10C Equations of Linear Relations Lesson 4
Math 10C Linear Equations Review
Комментарии
 0:05:09
0:05:09
 0:33:18
0:33:18
 0:29:54
0:29:54
 0:07:13
0:07:13
 0:17:37
0:17:37
 0:18:09
0:18:09
 0:32:23
0:32:23
 0:32:05
0:32:05
 0:14:32
0:14:32
 0:23:58
0:23:58
 0:05:37
0:05:37
 0:04:20
0:04:20
 0:05:15
0:05:15
 0:06:17
0:06:17
 0:13:30
0:13:30
 0:26:50
0:26:50
 0:29:13
0:29:13
 0:10:10
0:10:10
 0:26:11
0:26:11
 0:10:52
0:10:52
 0:01:48
0:01:48
 0:23:08
0:23:08
 0:19:52
0:19:52
 0:26:14
0:26:14