filmov
tv
Find the length x #thinkoutsidethebox #geometryskills #mathpuzzles
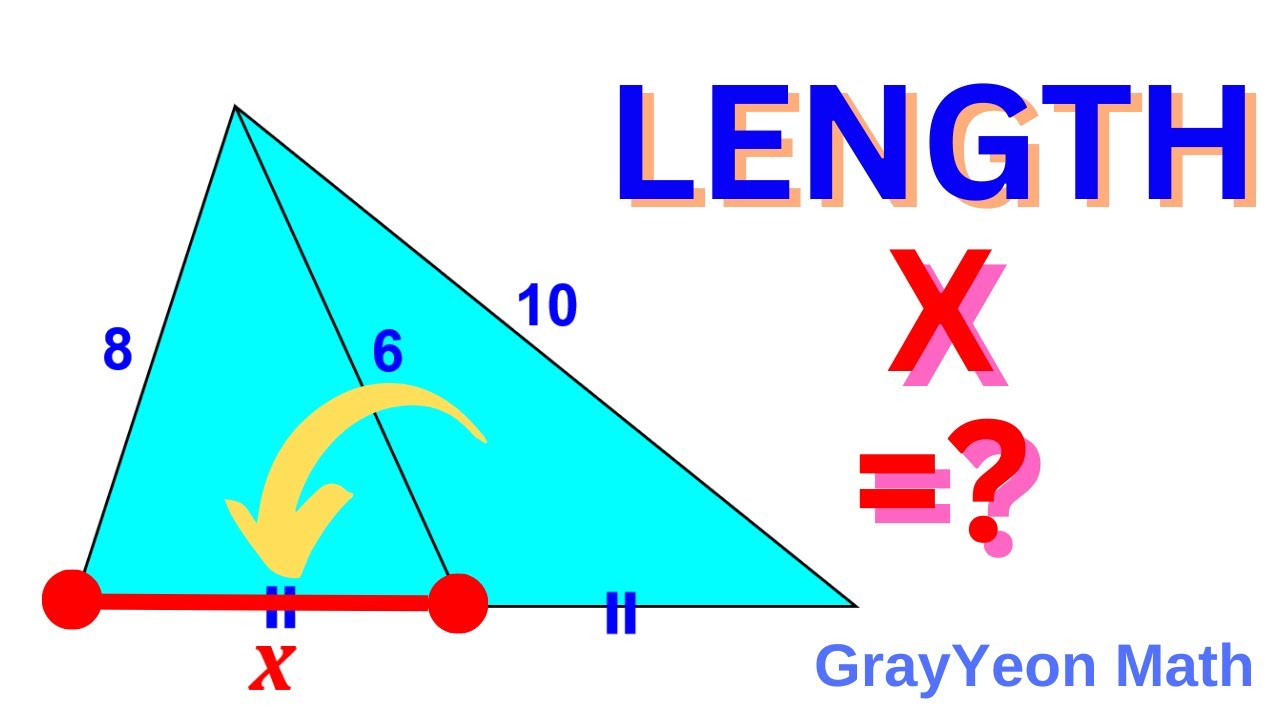
Показать описание
Find the length x #geometryskills #mathpuzzles #thinkoutsidethebox
This will be so much appreciated.
This will be so much appreciated.
Can you find the length X? | (How to think outside the Box) | #math #maths | #geometry
Find the length x #thinkoutsidethebox #geometryskills #mathpuzzles
Can you find the side length X of the polygon? | (Think outside the Box) |#math #maths | #geometry
Let's Think outside the Box! | Calculate the length X | (Nice explanation) | #math #maths
Calculate the side length X | How to Think outside the Box? | Important Geometry skills explained
Find the length x #geometryskills #mathpuzzles #thinkoutsidethebox #pythagoras_theorem
Find the length x #geometryskills #mathpuzzles #thinkoutsidethebox
Find the length x Important Geometry skills explained #geometryskills #thinkoutsidethebox
Find the length of the segment x #mathpuzzles #thinkoutsidethebox #geometryskills
Find the area of the triangle and the length x #geometryskills #mathpuzzles #thinkoutsidethebox
Find the length X | A Nice Geometry Problem | Important Geometry and Algebra Skills Explained
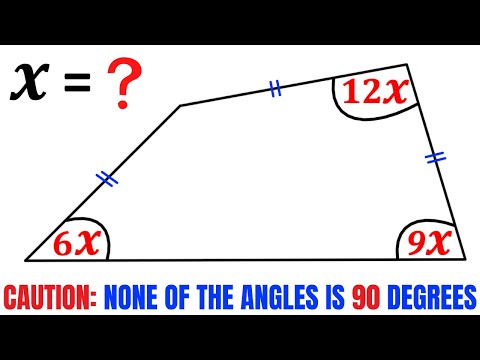
Find Side Length X of this Quadrilateral | Fast & Easy Tutorial
FInd the length of the segment AB #thinkoutsidethebox #geometryskills #mathpuzzles #GrayYeonMath
Find the area of the square and length x #geometryskills #mathpuzzles #thinkoutsidethebox
Neat Geometry | Can you find the length X? | (Math skills explained Step-by-Step) | #math #maths
Math Olympiad | Find missing side length X of the triangle | (Centroid and Medians) | #math #maths
Find the length x Important Geometry skills explained #geometryskills #mathpuzzles
Can you find the length X? | Semicircle in a square | (Crucial Math skills explained) | #math #maths
Find the length of the segment #mathpuzzles #geometryskills #thinkoutsidethebox
Two Methods | Find the missing side length X | (step-by-step explanation) | #math #maths
Find the length x | Important Geometry skills explained #geometryskills #mathpuzzles
Find the angle X and justify | Think outside the Box | Learn how to solve Geometry problem quickly
Find The Length X | Nice Geometry Question
Find the length x Important Geometry skills explained #geometryskills #mathpuzzles
Комментарии
 0:08:08
0:08:08
 0:08:26
0:08:26
 0:06:53
0:06:53
 0:08:18
0:08:18
 0:05:17
0:05:17
 0:04:57
0:04:57
 0:18:34
0:18:34
 0:10:33
0:10:33
 0:14:40
0:14:40
 0:15:47
0:15:47
 0:08:39
0:08:39
 0:06:07
0:06:07
 0:12:07
0:12:07
 0:08:03
0:08:03
 0:08:07
0:08:07
 0:08:09
0:08:09
 0:03:40
0:03:40
 0:09:35
0:09:35
 0:03:47
0:03:47
 0:08:44
0:08:44
 0:11:02
0:11:02
 0:08:18
0:08:18
 0:03:25
0:03:25
 0:04:48
0:04:48