filmov
tv
Schwarzschild geodesics - 12

Показать описание
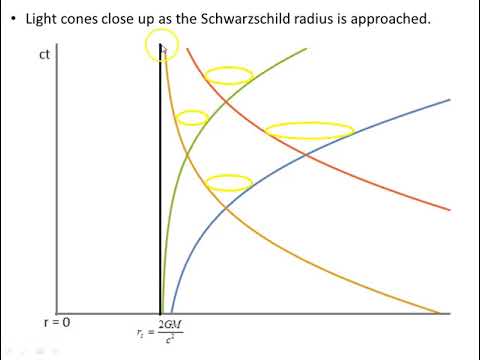
This video investigates the radial motion of photons in a Schwarzschild space-time for both the ingoing and outgoing directions. It does this using plots of these geodesics and shows how the local light cones behave in this geometry. The region within the Schwarzschild radius is investigated where the light cones tip over and point towards the singularity.
Schwarzschild geodesics - 12
General Relativity - Lecture 27 - Geodesics of Schwarzschild
What is General Relativity? Lesson 25: The Geodesics of Schwarzschild spacetime Part 4
What is General Relativity? Lesson 23: The Geodesics of Schwarzschild spacetime Part 2
What is General Relativity? The Geodesics of Schwarzschild spacetime Part 3
12 General Relativity Light Cones and Radial Motion in the Schwarzschild Metric
Relativity 108b: Schwarzschild Metric - Interpretation (Gravitational Time Dilation, Event Horizon)
Computing Radial Null Geodesics in Schwarzschild Geometry
Schwarzschild geodesics - 11
General Relativity, Lecture 23: null geodesics for the Schwarzschild metric
Relativity 108a: Schwarzschild Metric - Derivation
GRSS 164 Schwarzschild metric
What is General Relativity? Lesson 73: Solving for the Schwarzschild Metric Part 1 of 2
Schwarzschild geodesics - 10
Schwarzschild geodesics - 2
Schwarzschild geodesics - 9 (corrected)
Schwarzschild geodesics - 7
Schwarzschild geodesics - 5
Chapter 1.4 The Schwarzschild solution
Schwarzschild geodesics - 6
General Relativity Lecture 19: Geodesics in the Schwarzschild Geometry and Tests of GR
13. Schwarzschild Geometry (General Relativity)
The Geometry of a Black Hole
Stephen Crothers: General Relativity – a Case Study in Numerology | EU2015
Комментарии
 0:13:01
0:13:01
 1:28:38
1:28:38
 0:35:12
0:35:12
 0:45:06
0:45:06
 0:50:48
0:50:48
 0:24:35
0:24:35
 0:33:52
0:33:52
 0:04:29
0:04:29
 0:23:48
0:23:48
 0:42:39
0:42:39
 0:30:48
0:30:48
 0:12:23
0:12:23
 0:52:36
0:52:36
 0:09:44
0:09:44
 0:13:27
0:13:27
 0:15:37
0:15:37
 0:08:28
0:08:28
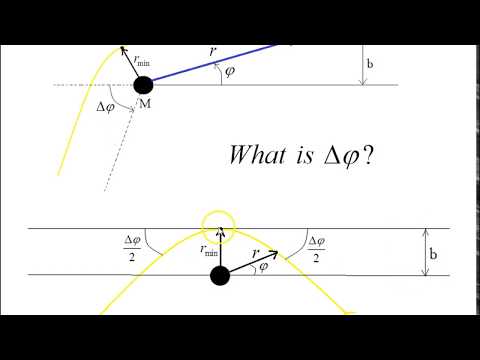 0:18:44
0:18:44
 0:56:26
0:56:26
 0:13:33
0:13:33
 1:07:16
1:07:16
 0:47:53
0:47:53
 0:18:31
0:18:31
 0:49:37
0:49:37