filmov
tv
Ecuaciones de grado mayor que tres, x²²=(x+6)¹¹
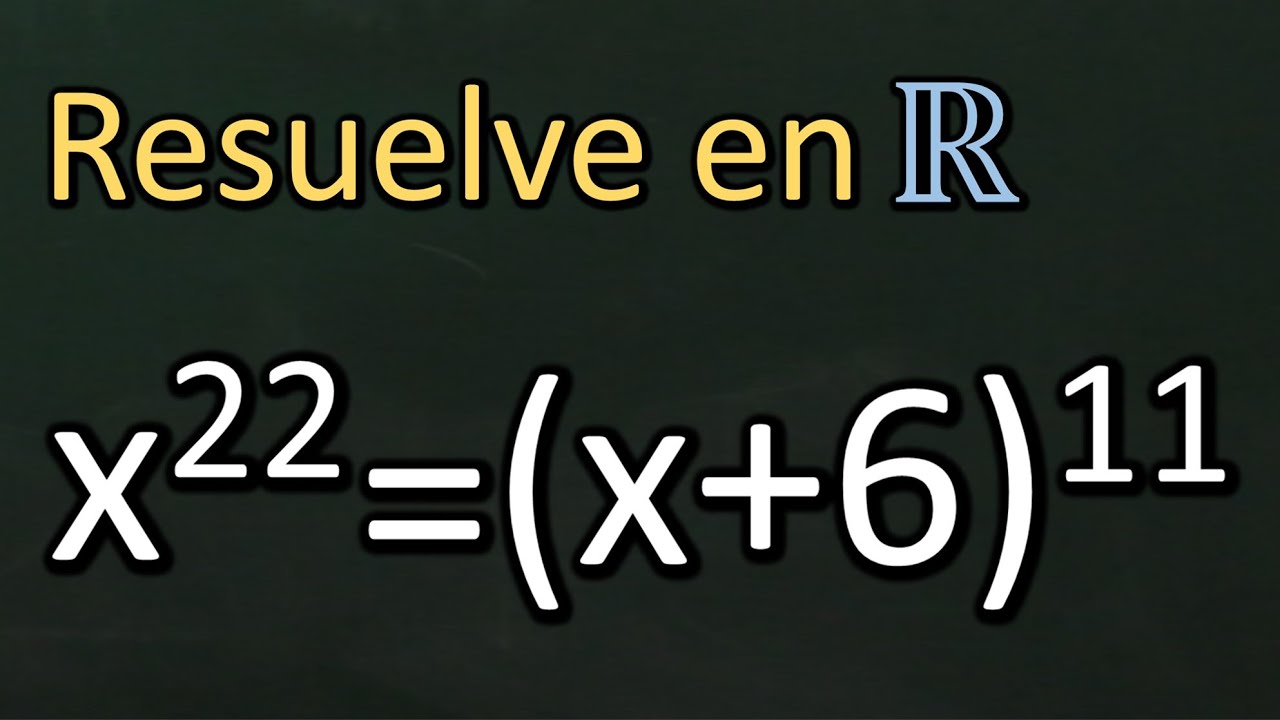
Показать описание
Resolución de ecuaciones de grado mayor que tres, en concreto tenemos x²²=(x+6)¹¹. La técnica usada consiste en intentar expresar ambos miembros en función de mismo exponente. Una vez hecho esto, usamos radicales para eliminar el grado de la ecuación.
Al final tendremos que resolver una ecuación de segundo grado. La resolución es en R.
#algebra #matematicas #matematicasconjuan
Al final tendremos que resolver una ecuación de segundo grado. La resolución es en R.
#algebra #matematicas #matematicasconjuan
Ecuaciones de grado superior a dos. Todosobresaliente.com
Ecuaciones de grado mayor que 2
ECUACIONES BICUADRADAS ✅
ECUACIONES de GRADO MAYOR que 2
Ecuaciones de grado mayor que tres, x²²=(x+6)¹¹
ECUACIONES DE GRADO MAYOR QUE DOS
Ecuaciones de grado mayor que 2.
CÓMO RESOLVER ECUACIONES DE TERCER GRADO. Método o regla de Ruffini
Aplicacion ecuaciones de grado superior
ECUACIONES DE GRADO MAYOR QUE 2
ECUACIONES POLINÓMICAS de GRADO MAYOR QUE 2 (paso a paso)
Formas de resolver ecuaciones de grado mayor a 2
Ecuaciones polinómicas de grado 5
Ecuaciones de grado mayor que 2
💚 Ecuaciones polinómicas de GRADO MAYOR QUE DOS (Ruffini) 💚 Secundaria ➡ Explicación y ejemplos...
ECUACIONES SÚPER FÁCIL
Ecuaciones de grado mayor o igual a 2
Resolución de Ecuaciones de Grado Mayor que Dos por Factorización: Consejos Prácticos y Ejemplos
Factorización por evaluación usando División Sintética, Ruffini | Ejemplo 1
Ecuaciones polinómicas de grado mayor que 2
Ecuaciones de grado mayor que dos
Cómo resolver una ecuación de grado mayor o igual que tres
💪ECUACIONES DE TERCER GRADO CAG*NDO LECHES😈
ECUACIONES DE GRADO MAYOR QUE 2
Комментарии
 0:26:35
0:26:35
 0:13:52
0:13:52
 0:09:56
0:09:56
 0:12:52
0:12:52
 0:06:38
0:06:38
 0:05:12
0:05:12
 0:08:29
0:08:29
 0:14:31
0:14:31
 0:07:40
0:07:40
 0:11:51
0:11:51
 0:10:10
0:10:10
 0:07:19
0:07:19
 0:05:20
0:05:20
 0:10:12
0:10:12
 0:13:43
0:13:43
 0:00:45
0:00:45
 0:12:58
0:12:58
 0:13:30
0:13:30
 0:15:12
0:15:12
 0:18:01
0:18:01
 0:09:28
0:09:28
 0:05:47
0:05:47
 0:00:58
0:00:58
 0:11:13
0:11:13