filmov
tv
Finding the nontrivial zeros of the Riemann Zeta Function using Desmos

Показать описание
In this video I discuss extending the Riemann Zeta Function using the Dirichlet Eta Function, and use this along with Desmos to find the first few nontrivial zeros.
All nontrivial zeros of the Riemann Zeta Function so far calculated by humans (there are about 10^13 of them) all have real part 1/2, which falls in line with the Riemann Hypothesis which says that all of these zeros have real part 1/2.
The Riemann Hypothesis is a currently unsolved math problem, and is attached to a $1,000,000 prize awarded by the Clay Mathematics Institute.
All nontrivial zeros of the Riemann Zeta Function so far calculated by humans (there are about 10^13 of them) all have real part 1/2, which falls in line with the Riemann Hypothesis which says that all of these zeros have real part 1/2.
The Riemann Hypothesis is a currently unsolved math problem, and is attached to a $1,000,000 prize awarded by the Clay Mathematics Institute.
Finding the nontrivial zeros of the Riemann Zeta Function using Desmos
Where are all the nontrivial zeros?
The Search for Siegel Zeros - Numberphile
How to calculate nontrivial zero of zeta function from R.O.S.E.
First several non-trivial zeros of the Riemann Zeta function
Complex Integration and Finding Zeros of the Zeta Function
The Riemann Hypothesis, Explained
But what is the Riemann zeta function? Visualizing analytic continuation
Non - trivial Solution | Matrix | JEE Main - 2021 @ARYA_Mathematics #jeemainspyq
Reimann Hypothesis Non-Trivial Zeros
The Key to the Riemann Hypothesis - Numberphile
Riemann zeta function, real and imaginary graphs with non-trivial zeros
Riemann Hypothesis - Confirming the non-trivial zeros
Nontrivial Zeros of the Riemann Zeta Function Know a lot
zero of zeta function
Top 5 Riemann Zeta Function Zeros
The reason of why all non trivial zero of zeta function on line x=1/2
Nontrivial zero of Riemann hypothesis
What is the Riemann Hypothesis REALLY about?
The High Schooler Who Solved a Prime Number Theorem
Homogeneous Systems of Linear Equations - Trivial and Nontrivial Solutions, Part 1
Trivial zero of zeta function ; origin of non trivial zero of zeta function.
Trivial Zero Zeta function, how to find Zera trywialne jak je znaleźc.
The distribution of primes and zeros of Riemann's Zeta function - James Maynard
Комментарии
 0:24:56
0:24:56
 0:15:53
0:15:53
 0:16:27
0:16:27
 0:00:24
0:00:24
 0:02:16
0:02:16
 0:52:49
0:52:49
 0:16:24
0:16:24
 0:22:11
0:22:11
 0:06:25
0:06:25
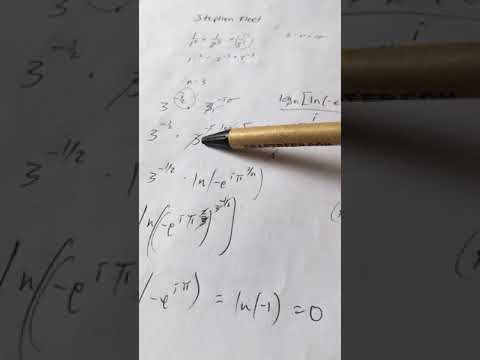 0:03:36
0:03:36
 0:12:38
0:12:38
 0:00:37
0:00:37
 0:15:37
0:15:37
 0:48:16
0:48:16
 0:00:28
0:00:28
 0:01:35
0:01:35
 0:00:24
0:00:24
 0:06:46
0:06:46
 0:28:33
0:28:33
 0:05:15
0:05:15
 0:09:09
0:09:09
 0:04:15
0:04:15
 0:06:41
0:06:41
 0:12:33
0:12:33