Albert Atserias: Towards an algorithmic theory of proof complexity

Friday Sep 30, 2022
Towards an algorithmic theory of proof complexity
(Albert Atserias, Universitat Politècnica de Catalunya)

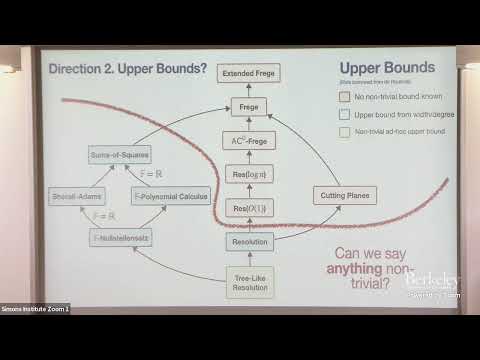
A possibly unexpected by-product of the mathematical study of the lengths of proofs, as is done in the field of propositional proof complexity, is, I claim, that it may lead to new algorithmic insights. To explain this, I will first recall the origins of proof complexity as a field. Then I will explain why our current understanding of certain proof systems could lead to new algorithms. The key to this is that, for several proof systems of practical use, the class of tautologies with low-complexity proofs comes with a tight semantic characterization. Concretely, the characterization states that a tautology fails to have a low-complexity proof precisely when it is locally falsifible, in a precise technical sense of the term. One immediate derivative of this is that, for those proof systems that admit such semantic characterizations, the statement that a formula has a low-complexity proofs has: (1) low-complexity certificates when true, and (2) low-complexity refutations when false. We illustrate the point by discussing the recently discovered subexponential-time algorithm that distinguishes the graphs that are 3-colorable from those that are not even n^eps-colorable in time exp(n^{1-2eps}), which beats all previously known approaches.