Miller indices for hexagonal structures. Why and how we use 4 indices.

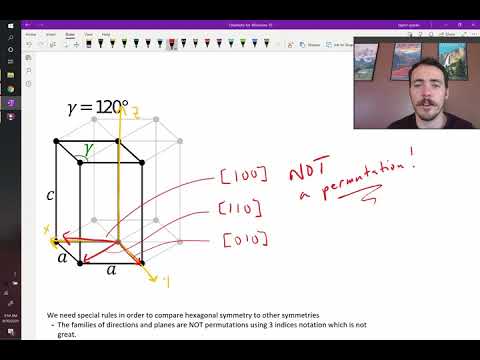
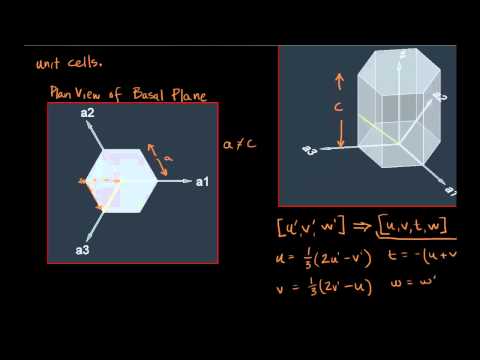
Miller indices are a super useful way of identifying points, directions, and planes in crystal structures. Miller indices can also denote families of equivalent planes and directions. In non-cubic systems its easy to identify all members of the family by identifying permutations of the miller indices including both positive and negative values. For example, the 100 family includes -100, 100, 010, 0-10, 001, and 00-1. The problem with hexagonal crystal structures CANNOT generate all family members by using permutations when we use the traditional 3 indix Miller notation. Instead, we need a new system with 4 indices based on 4 axes. This video shows how this works.

[derlynmudombi]

Very straightforward and understandable 🙌🙌🙃my go-to guy for mse concepts

[MykeAndThoseGuys]

This Explained it perfectly! thank you!

[TheYesyouare]

thanks for the excellent explanation! One question though - couldn't you also say [0010] instead of [1, 1, -2, 0]? How is this redundancy handled?

[alejandrocielo]

And on the other hand, how would it be?PToPas To change the IM from hexagonal to cubic, I can't understand that.
nice video

[coreyfarrell]

In the beginning of the video you said the 3 índice was [110], then later in the same direction, you label it [100]. I’m confused

[herbmuell]

According to Ashcroft & Mermin, Miller indices are used for the reciprocal lattice only, so (101) and {101} are Miller indices. A&M call [101] and <101> just directions in the direct lattice, and that's what you are doing. So I am a little bit confused by the title of your video. Otherwise very good, thanks a lot.

[goahead]

I used this method to do the opposite direction calculation. [012] -> [-12-16], it's not correct!!

[derlynmudombi]

Very straightforward and understandable 🙌🙌🙃my go-to guy for mse concepts