filmov
tv
Find all positive integers n such that n!+2023 is a perfect square.

Показать описание
The video illustrates step-by-step how to find all positive integers n such that n!+2023 is a perfect square. Use proof by contradiction to prove that n!+2023 can't be a perfect square when n is greater than 3.
Subscribe at:
#MathsEnhancer #MathematicalCompetition #MathematicalOlympiad #ChallengingMathematicsProblems #MathematicsCompetition #EnhanceMathematicsProblemSolvingSkills #Mathematics
#ImproveMathematicsGrades
Proof by contradiction
modulo operation in maths
proof by contradiction examples
proof by contradiction a level maths aqa
Modulo operation
Perfect square
Perfect square numbers
Challenging mathematics problems
Enhance mathematics problem solving skills
Improve mathematics grades
Olympics math
Olympics maths
Olympics mathematics
Olympics math competition
Math Olympiad training
International Mathematical Olympiad questions and solutions
International Mathematical Olympiad questions and answers
How to solve Olympiad question
How to solve International Mathematical Olympiad question
How to solve Olympiad Mathematics Question
How to prepare for Maths Olympiad
How to prepare for Math Olympiad
Olympiad mathematics competition
Olympiad exam
Olympiad exam sample paper
Maths Olympiad sample question
Maths Olympiad sample answer
Math Olympiad
Subscribe at:
#MathsEnhancer #MathematicalCompetition #MathematicalOlympiad #ChallengingMathematicsProblems #MathematicsCompetition #EnhanceMathematicsProblemSolvingSkills #Mathematics
#ImproveMathematicsGrades
Proof by contradiction
modulo operation in maths
proof by contradiction examples
proof by contradiction a level maths aqa
Modulo operation
Perfect square
Perfect square numbers
Challenging mathematics problems
Enhance mathematics problem solving skills
Improve mathematics grades
Olympics math
Olympics maths
Olympics mathematics
Olympics math competition
Math Olympiad training
International Mathematical Olympiad questions and solutions
International Mathematical Olympiad questions and answers
How to solve Olympiad question
How to solve International Mathematical Olympiad question
How to solve Olympiad Mathematics Question
How to prepare for Maths Olympiad
How to prepare for Math Olympiad
Olympiad mathematics competition
Olympiad exam
Olympiad exam sample paper
Maths Olympiad sample question
Maths Olympiad sample answer
Math Olympiad
Find All Positive Integers (a,b,c) - China Girls Math Olympiad 2023
Can you find all positive integers n to make the expression a perfect square?
Find all positive integers n that will make n²+45 perfect square
Find All Possible Positive Integers (n, m) --- BMO 2016
Find all positive integers n such that n!+2023 is a perfect square.
Find all positive integers n such that this expression is an integer
(Number Theory) Find all positive integers n for which n! + 5 is a perfect cube
Find all positive integers n for which the given statement is not true. 2^nn^2
Differential Equations: PDEs and BVPs, Heat Equation motivates Fourier expansion, 12-2-24
Prove that 2^n is greater than n for all positive integers n | Mathematical Induction | Maths
Find all positive integers, n , such that (193n + 8)/(n^2 + 14) a natural number, like Finland 2001
Find all Positive integers n for which (n² + 45) is a Perfect Square | Unique Problem In Mathematics...
Find all positive integers n such that n*2^n + 1 is a perfect square
Summing positive integers with triangles
Find all positive integers n for which one number can be perfect square
Induction Divisibility
sum of first n positive integers formula #shorts #youtubeshorts #ytshorts #viralshorts #trending
Find all positive integers n such that 3^2n+3n^2+7 is a perfect square
Find all integers a such that (4a+1)/(2a-7) is an integer
Find the sum of all positive integers n, satisfying root of the sum of n^2 and 1203 is an integer.
Prove that (n!)^2 ≤ n^n.n! for all positive integers | Factorial Notation | PnC | Math | Problem
Irish Mathematical Olympiad | 2009 Q3
FIND THE POSITIVE INTEGERS - FACTORIZATION IS THE KEY #shorts #maths #equations #integers
Find all positive integers x,y,z satisfying x^y^z.y^z^x.z^x^y=5xyz
Комментарии
 0:07:57
0:07:57
 0:03:21
0:03:21
 0:05:57
0:05:57
 0:05:04
0:05:04
 0:10:50
0:10:50
 0:02:06
0:02:06
 0:01:53
0:01:53
 0:00:33
0:00:33
 0:47:04
0:47:04
 0:07:30
0:07:30
 0:09:07
0:09:07
 0:06:25
0:06:25
 0:10:23
0:10:23
 0:00:35
0:00:35
 0:05:11
0:05:11
 0:20:35
0:20:35
 0:01:01
0:01:01
 0:06:09
0:06:09
 0:02:29
0:02:29
 0:05:06
0:05:06
 0:06:25
0:06:25
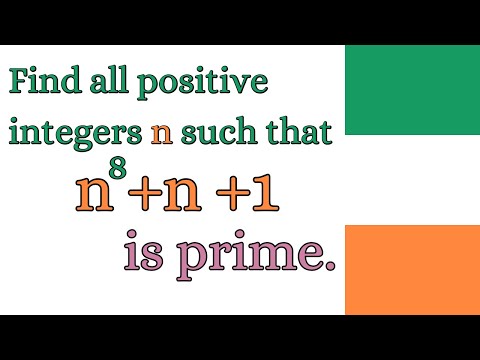 0:12:47
0:12:47
 0:00:08
0:00:08
 0:02:53
0:02:53