filmov
tv
Find a solution to the differential equation y''-y=sinh x
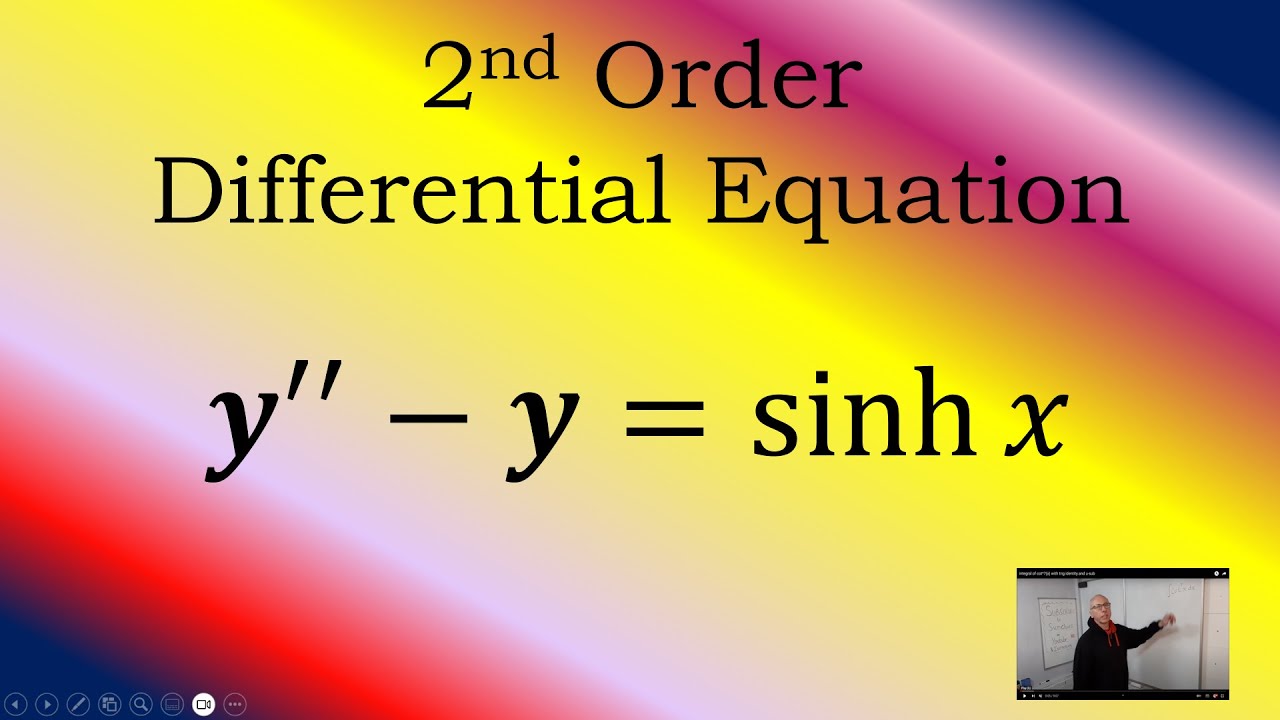
Показать описание
Here we solve for y(x) from a second order linear differential equation.
y''(x)-y(x)=sinh(x)
here we find the homogeneous solution setting y''-y=0.
Then we find a particular solution but setting sinh(x) to its exponential identity of 1/2(e^x-e^-x) .
That way we can use a system of corresponding coefficients to solve.
The solution is the homogeneous solution plus the particular solution.
y(x) is our dependent variable as it depends on x.
x is our independent variable
#functionalanalysis
#functional
#calculus
#calculusofvariations
#calculusofvariation
#multivariablecalculus
#multivariable
#partial_differentiation
#partialderivatives
#partialdifferentiation
y''(x)-y(x)=sinh(x)
here we find the homogeneous solution setting y''-y=0.
Then we find a particular solution but setting sinh(x) to its exponential identity of 1/2(e^x-e^-x) .
That way we can use a system of corresponding coefficients to solve.
The solution is the homogeneous solution plus the particular solution.
y(x) is our dependent variable as it depends on x.
x is our independent variable
#functionalanalysis
#functional
#calculus
#calculusofvariations
#calculusofvariation
#multivariablecalculus
#multivariable
#partial_differentiation
#partialderivatives
#partialdifferentiation
 0:00:24
0:00:24
 0:00:24
0:00:24
 0:04:36
0:04:36
 0:01:19
0:01:19
 0:02:36
0:02:36
 0:02:37
0:02:37
 0:03:02
0:03:02
 0:02:03
0:02:03
 0:01:47
0:01:47
 0:01:40
0:01:40
 0:08:54
0:08:54
 0:00:06
0:00:06
 0:08:21
0:08:21
 0:04:17
0:04:17
 0:02:19
0:02:19
 0:05:47
0:05:47
 0:03:28
0:03:28
 0:06:30
0:06:30
 0:09:39
0:09:39
 0:06:26
0:06:26
 0:00:53
0:00:53
 0:02:31
0:02:31
 0:31:25
0:31:25
 0:03:58
0:03:58