filmov
tv
when 'normal' trig functions aren't enough -- the Clausen function.

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
when 'normal' trig functions aren't enough -- the Clausen function.
Evaluate the composition of trigonometric functions not on the unit circle
What does sine actually mean?
How to cheat on test using your calculator #viral #shorts
Inverse Trigonometric Functions
The definition of a derivative
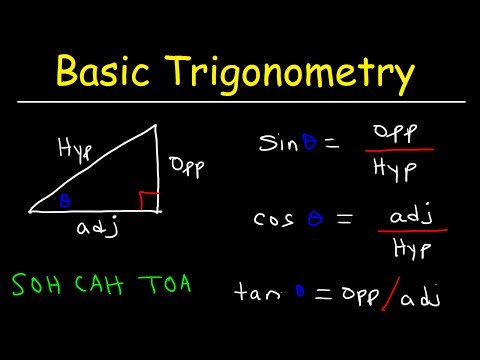
Trigonometry For Beginners!
Hyperbolic Functions: Definitions, Identities, Derivatives, and Inverses
LOOKS TOUGH UNTIL YOU SEE THIS...😏 | JEE 2026
trigonometry 0 to 360 #education #learning #mathmatics #mathstricks #mathhack #viral
The complex relationship between regular and hyperbolic trig functions
Tangents, Normals and Trig Functions
How to solve Non-Right Angled Triangles using Sine
Hyperbolic Trig Functions - Basic Introduction
Trigonometry -- More Applications of Trig Functions
Trigonometry made easy
Model Monthly Temperature Solve Sinusoidal Trigonometric Equation
Trigonometry: Comparing Inverse Trig Functions and Regular Trig Functions
Derivatives of Trigonometric Functions
How To Graph Trigonometric Functions | Trigonometry
Zero Positive Negative Average Rate of Change Sinusoidal Trig Function
How to Graph a Trig Function : Math-Tastic
Differentiation and Integration formula
JEE Aspirants ka Sach 💔 #JEE #JEEMain #Shorts
Комментарии
 0:17:41
0:17:41
 0:03:29
0:03:29
 0:01:00
0:01:00
 0:00:27
0:00:27
 0:06:54
0:06:54
 0:01:00
0:01:00
 0:21:52
0:21:52
 0:07:34
0:07:34
 0:06:41
0:06:41
 0:00:05
0:00:05
 0:16:23
0:16:23
 0:10:46
0:10:46
 0:07:47
0:07:47
 0:10:12
0:10:12
 0:57:03
0:57:03
 0:12:43
0:12:43
 0:10:43
0:10:43
 0:09:29
0:09:29
 0:05:27
0:05:27
 0:22:37
0:22:37
 0:04:11
0:04:11
 0:02:18
0:02:18
 0:00:06
0:00:06
 0:00:12
0:00:12