filmov
tv
Vector calculus in curvilinear coordinates! (a helpful intro)
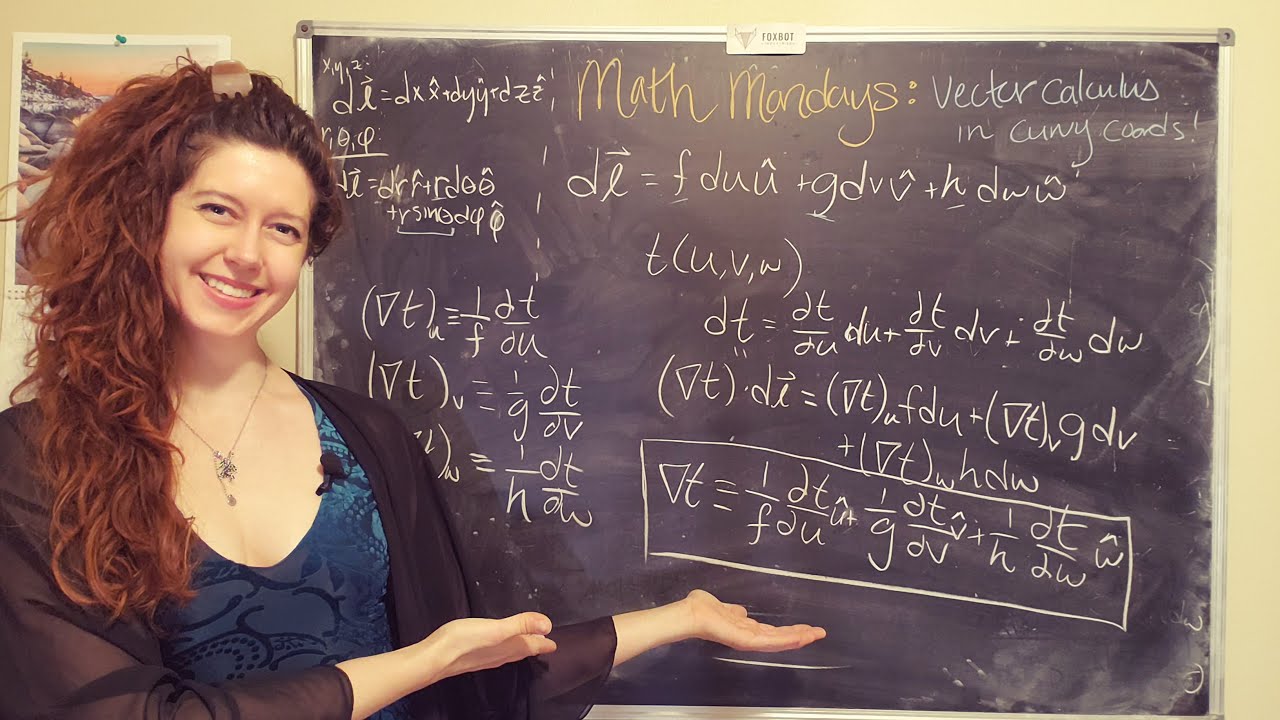
Показать описание
In this video, we learn about how to do derivatives, or differential calculus, in different types of coordinate systems, like spherical coordinates! We'll focus on the gradient of a function.
Rather than simply giving you the equations (you can look them up!), we will look at *where* the equations come from by building out a generic coordinate system to figure out how we translate the gradient.
Questions about this or other math topics? Leave a comment and let's tackle it together!
Rather than simply giving you the equations (you can look them up!), we will look at *where* the equations come from by building out a generic coordinate system to figure out how we translate the gradient.
Questions about this or other math topics? Leave a comment and let's tackle it together!
Vector calculus in curvilinear coordinates! (a helpful intro)
An Introduction to Curvilinear Coordinates in Differential Geometry
The Del Operator in spherical coordinates | Lecture 34 | Vector Calculus for Engineers
Tutorial on vector calculus and curvilinear coordinates
Curvilinear Coordinates: Vector Calculus #8.1 | ZC OCW
Lec. 01 | Introduction to Curvilinear Coordinates | Suppose Math with Akhtar Abbas
Definition of spherical coordinates | Lecture 33 | Vector Calculus for Engineers
Integration in Spherical Coordinates
Differential vector calculus in curvilinear coordinate systems
Physics Ch 67.1 Advanced E&M: Review Vectors (73 of 113) Spherical Coordinates
GOPH 547 - Topic M5d - Vector Operator in Curvilinear Coordinates
Coordinate Transformations and Curvilinear Coordinates | Tensor Calculus
#Curvilinear_co_ordinates #Vector_Calculus ||Unit Vectors Along Tangent & Normal in Curvilinear
PHYS 2500 Quiz 3: Vector Calculus in Curvilinear Coordinates
Curvilinear coordinate system (vector calculus)
Cylindrical coordinates | Lecture 32 | Vector Calculus for Engineers
SPHERICAL COORDINATES//CURVILINEAR COORDINATES//VECTOR CALCULUS//INTRODUCTION TO ELECTRODYNAMICS
Vector Calculus- #9(Orthogonal Curvilinear Coordinates ) For IIT JAM, JEST, BSc, CSIR NET etc
Ch3 vector calculus | part1 | cartesian , cylindrical and spherical coordinates
Calculus 3 Lecture 11.7: Using Cylindrical and Spherical Coordinates
Deriving Spherical Coordinate Unit Vectors (with Geometric Interpretation)
Polar Coordinates (Gradient) | Lecture 26 | Vector Calculus for Engineers
Polar Coordinates | Lecture 24 | Vector Calculus for Engineers (V1)
PHYS 2500 Lec 8: Derivative Calculus in Curvilinear Coordinates
Комментарии
 0:11:43
0:11:43
 0:22:44
0:22:44
 0:06:43
0:06:43
 0:21:25
0:21:25
 0:50:48
0:50:48
 0:36:30
0:36:30
 0:06:51
0:06:51
 0:07:52
0:07:52
 0:14:00
0:14:00
 0:10:57
0:10:57
 0:19:13
0:19:13
 0:11:48
0:11:48
 0:35:12
0:35:12
 0:21:04
0:21:04
 0:22:07
0:22:07
 0:08:17
0:08:17
 0:53:28
0:53:28
 0:18:02
0:18:02
 0:20:48
0:20:48
 1:40:16
1:40:16
 0:04:09
0:04:09
 0:12:25
0:12:25
 0:15:13
0:15:13
 1:09:39
1:09:39