filmov
tv
integral of floor of x from 0 to 4 (greatest integer function)

Показать описание
Here we will integrate floor(x) from 0 to 4. The floor function is also called the greatest integer function.
10% off with the code "TEESPRINGWELCOME10"
Equipment:
---------------------------------------------------------------------------------------------------
10% off with the code "TEESPRINGWELCOME10"
Equipment:
---------------------------------------------------------------------------------------------------
integral of floor of x from 0 to 4 (greatest integer function)
Integral of floor(x) ?!
Integral of floor(x)
This integral will have you on the floor 🤣🤣
Integral Battle! With Floor Functions
Integral of Floor Function of Natural Log - Geometry | Integration | Calculus | Glass of Numbers
Integral of floor(x)e^(-x) from 0 to infinity
ZETA IN DISGUISE- An Awesome Floor Function Integral!
Integral of floor function
Calculus | Find the Integral of the Floor Function of x
Calculus | Find the Integral of the Floor Function of Square of x
Calculus | Find the Integral of the Floor Function of x+1
A wonderful floor integral connected to the Basel problem
Floor, Ceiling, Fractional part all in one integral problem
A floor integral leading to a nice result: int (0,1) x\floor(1/x)
A nice integral with floor function
Integral from 0 to 1 of 1/(1+floor(1/x))
Integral x(floor(x))(fractional part(x)) from 0 to n | Fractional part integral
Integral with the Exponential and Floor Functions (The Art of Integration)
This Integral Went Viral in USA | Integral xfloor(1/x)dx
Integral (floor(x) with non integer integration limit
Calculus | Find the Integral of the Floor Function of x^2
Calculus | Find the Integral of the Floor Function of 2x
Double Integral on a Floor Function, Integrate Floor(x^2+y^2)
Комментарии
 0:05:42
0:05:42
 0:03:27
0:03:27
 0:01:19
0:01:19
 0:03:29
0:03:29
 0:15:31
0:15:31
 0:22:24
0:22:24
 0:04:41
0:04:41
 0:11:23
0:11:23
 0:12:39
0:12:39
 0:06:45
0:06:45
 0:04:54
0:04:54
 0:05:33
0:05:33
 0:08:19
0:08:19
 0:08:24
0:08:24
 0:08:04
0:08:04
 0:02:37
0:02:37
 0:07:37
0:07:37
 0:06:26
0:06:26
 0:07:32
0:07:32
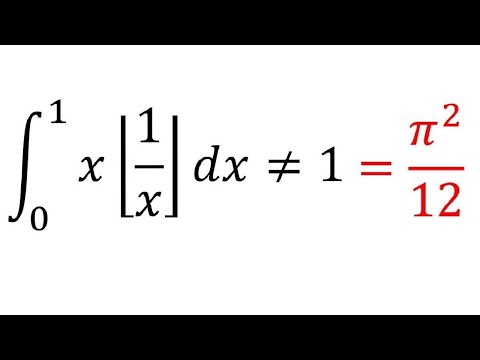 0:14:01
0:14:01
 0:08:31
0:08:31
 0:04:46
0:04:46
 0:09:33
0:09:33
 0:03:00
0:03:00