filmov
tv
Relativity 104f: Special Relativity - Relativistic Dynamics and 4-Vectors (E=mc^2)
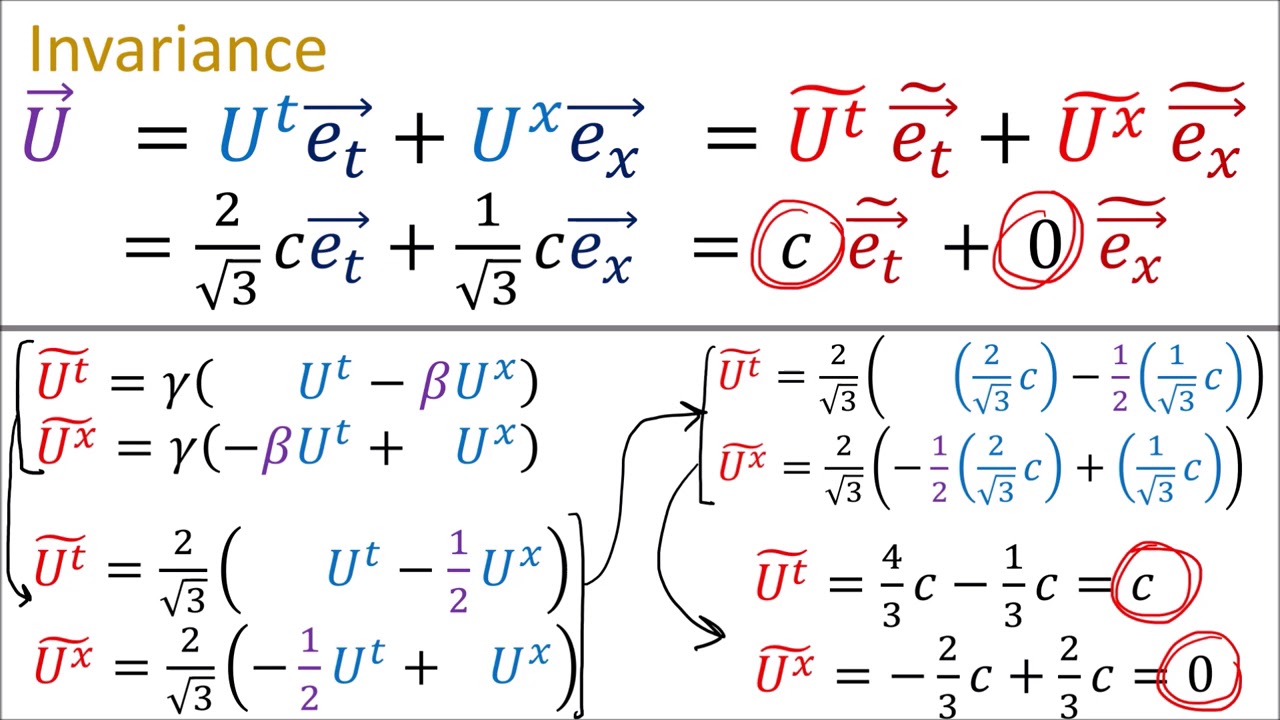
Показать описание
0:00 Intro (4-vectors and Invariance)
3:38 4-velocity derivation
9:07 4-velocity example
14:44 4-momentum derivation
21:25 4-momentum for light
24:07 4-momentum example
25:38 Conservation of 4-momentum
28:20 4-acceleration
31:42 4-force
32:44 Summary
Relativity 104f: Special Relativity - Relativistic Dynamics and 4-Vectors (E=mc^2)
Relativity 104e: Special Relativity - Spacetime Interval and Minkowski Metric
Relativity 101b: Introduction to Special Relativity
Relativity 104c: Special Relativity - Time Dilation and Length Contraction Geometry
Relativity 104b: Special Relativity - Lorentz Transform Equations Derivation
Relativity 104d: Special Relativity - Velocity Addition and Relativity of Simultaneity
Relativity 105a: Acceleration - Hyperbolic Motion and Rindler Horizon
How to use 4-Vectors and Lorentz Transformations in Special Relativity!
INTRODUCTION TO SPECIAL RELATIVITY. Lesson 28: the energy-momentum vector.
8.2 Introduction to 4-Vector Notation
Special Relativity: Relativistic Mechanics
Four-Vectors in special relativity
Acceleration in Special Relativity
Relativity 09.03. Defining Momentum in Special Relativity
Everything moves at the speed of light: Four-velocity in Special Relativity #PhysicsNextBook
What are FOUR VECTORS in Special Relativity? | 4-Vector Velocity, Acceleration, Momentum etc
Velocity in Special Relativity | Four-Velocity
Physics 10 - Questions and Exercises for Chapter 14, Special Relativity
Classroom Aid - Simultaneity Lost
Special Relativity 7 E&M
Momentum in Special Relativity | Four-Momentum
Relativistic Dynamics -- Problem 01
Special Relativity- Relativistic Dynamics: An Introduction
Relativity #19 - Introducing four velocity
Комментарии
 0:35:10
0:35:10
 0:34:19
0:34:19
 0:15:20
0:15:20
 0:31:36
0:31:36
 0:17:23
0:17:23
 0:23:10
0:23:10
 0:31:37
0:31:37
 0:16:01
0:16:01
 0:06:48
0:06:48
 0:05:45
0:05:45
 0:37:12
0:37:12
 1:29:40
1:29:40
 0:58:35
0:58:35
 0:10:15
0:10:15
 0:11:47
0:11:47
 1:01:54
1:01:54
 0:04:11
0:04:11
 0:27:35
0:27:35
 0:02:11
0:02:11
 0:15:23
0:15:23
 0:03:06
0:03:06
 0:08:00
0:08:00
 0:37:33
0:37:33
 0:13:04
0:13:04