filmov
tv
Factoring Polynomials Sum Difference of Cubes

Показать описание
I explain how to factor the Sum of Cubes and Difference of Cubes patterns and then work through many examples to help you understand the process. These are a special type of Polynomials.
Here you can find a selection of my Factoring Lessons
Here you can find a selection of my Factoring Lessons
How To Factor Difference of Squares - Algebra
Factoring sum of cubes | Polynomial and rational functions | Algebra II | Khan Academy
Factoring Polynomials Sum Difference of Cubes
Factoring Sum and Difference of Cubes
How to factor a polynomial using the difference of two cubes
Difference of cubes factoring | Polynomial and rational functions | Algebra II | Khan Academy
How To Factor Polynomials The Easy Way!
Factoring Polynomials - Difference of Two Squares - Polynomial Factoring
Recursion Relations and Generating Function of Hermite Polynomials
❖ Factoring Sums and Differences of Cubes ❖
Factoring Sum and Difference of Two Cubes - Mathematics 8
Factoring Polynomials (sum and difference of cubes)
Factoring a polynomial using the difference of two cubes
Factoring Trinomials & Polynomials, Basic Introduction - Algebra
learn how to factor using the difference of two cubes
Factoring using the difference of two squares with multiple variables
FACTORING SUM AND DIFFERENCE OF TWO SQUARES @MathTeacherGon
Factoring Sum Difference of Cubes
Intermediate Algebra Lecture 6.5: Factoring Binomials (Difference of Squares/Cubes)
10 - Factor Sum of Cubes and Difference of Cubes in Algebra, Part 1
Factor Polynomials - Understand In 10 min
SOAP:Factoring Sums and Differences of Cubes
Factoring Sum and Difference of Two Cubes
Factoring Difference of Cubes x^3 - 8
Комментарии
 0:19:35
0:19:35
 0:04:46
0:04:46
 0:11:01
0:11:01
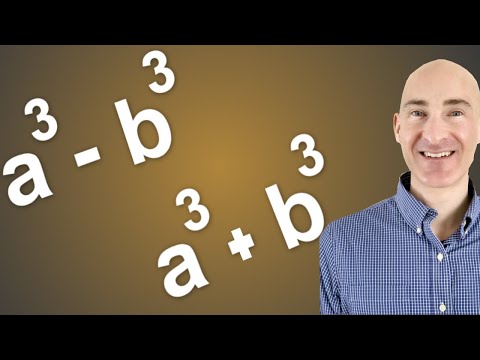 0:05:35
0:05:35
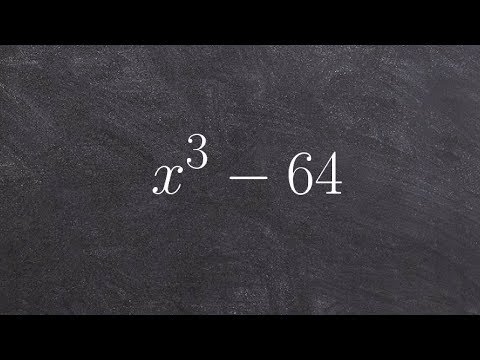 0:02:21
0:02:21
 0:04:12
0:04:12
 0:11:54
0:11:54
 0:08:19
0:08:19
 0:10:49
0:10:49
 0:05:54
0:05:54
 0:09:06
0:09:06
 0:13:46
0:13:46
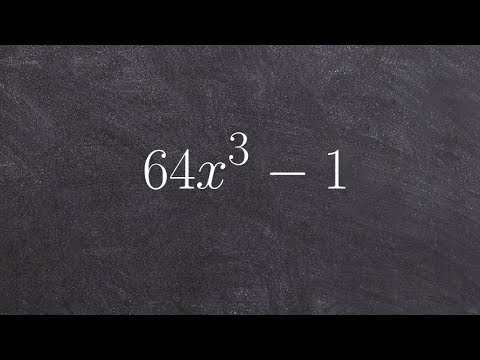 0:02:20
0:02:20
 0:34:46
0:34:46
 0:03:18
0:03:18
 0:02:25
0:02:25
 0:08:31
0:08:31
 0:07:44
0:07:44
 1:39:00
1:39:00
 0:20:28
0:20:28
 0:14:06
0:14:06
 0:03:46
0:03:46
 0:04:49
0:04:49
 0:01:19
0:01:19