Proof: Greater Angle is Opposite the Longer Side in a Triangle | Geometry

preview_player
Показать описание
If one side of a triangle is longer than another, then the angle opposite the longer side is greater than the angle opposite the shorter side. We prove this result in today's geometry video lesson. Note how this is a sort of extension of the isosceles triangle theorem, which tells us about angles opposite congruent sides, now we are addressing angles opposite non-congruent sides. The converse of this statement is true as well - that is: if an angle is greater than another in a triangle, then the side opposite the greater angle is longer than the side opposite the lesser angle. Try proving it yourself! #Geometry

Note this is Proposition 18 of Euclid's elements, the converse of Proposition 19.

Proof that the Longer Side is Opposite the Greater Angle: coming soon

★DONATE★

Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!

Follow Wrath of Math on...

  1. Wrath of Math
  2. wrath of math
  3. math lessons
  4. math
  5. education
  6. math video
Рекомендации по теме
Proof: Greater Angle 0:06:28

Proof: Greater Angle is Opposite the Longer Side in a Triangle | Geometry

Angle opposite to 0:05:17

Angle opposite to longer side is greater in a triangle | Proof | Theorem

Angle opposite to 0:11:22

Angle opposite to longer side is greater in a triangle (Theorem and Proof)

Proof: The Angle 0:05:54

Proof: The Angle of a Triangle Opposite The Longest Side is the Largest Angle

Side opposite to 0:10:11

Side opposite to greater angle is longer in a triangle (Theorem and Proof)

Prove that side 0:09:08

Prove that side opposite to the greater angle is longer – Inequalities in a triangle class 9

Class 9 | 0:03:07

Class 9 | Chapter 7 | Theorem 7.7 In a triangle, side opposite to greater angle is longer | NCERT

Prove that the 0:10:49

Prove that the angle opposite to the longer side is greater – Inequalities in a triangle class 9

Leaving Certificate Proof 0:09:27

Leaving Certificate Proof that the biggest angle is opposite the longest side in a triangle.

In any triangle 0:12:57

In any triangle ,Prove that the side opposite to the Greater angle is longer (Converse of Theorem1)

GCSE Maths - 0:05:36

GCSE Maths - Alternate, Corresponding and Allied Angles - Parallel Lines Angle Rules #117

In a triangle 0:04:12

In a triangle the greater angle has the longer side opposite to it. | 9 | CONGRUENT TRIANGLE | ...

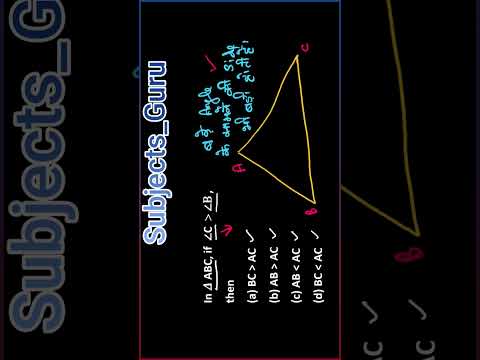
side opposite to 0:00:52

side opposite to greater angle is greater #shorts #triangles #subjects_guru #mathshorts

The Angle-Opposite-Side Relation 0:08:52

The Angle-Opposite-Side Relation

Exterior Angle Inequality 0:05:05

Exterior Angle Inequality Theorem With Two Column Proofs - Geometry

In Any Triangle 0:08:05

In Any Triangle The Side Opposite To The Larger Angle is Longer | Triangles Class 9 Theorem 7.7

Prove that in 0:02:51

Prove that in a triangle, other than an equilateral triangle, angle opposite to the longest side ...

Side opposite greater 0:02:54

Side opposite greater angle is longer

In a Triangle, 0:03:31

In a Triangle, sides opposite to larger angle are larger || PROOF ||

Side opposite to 0:01:49

Side opposite to greatest angle is greatest

Proof of Prop 0:09:23

Proof of Prop I 18 Inequality of Opposite Sides an Angles

Angle opposite to 0:02:13

Angle opposite to greatest side is greatest

Class 9 | 0:06:08

Class 9 | Chapter 7 | Theorem 7.6 In a triangle, angle opposite to larger side is greater | NCERT

Triangles | Theorem 0:01:51

Triangles | Theorem 7.7 | Class IX |Side opposite to the larger angle is longer | Maths| Excitonium

Комментарии
Автор

Very nice! I also like that you mentioned AP can be constructed equal to AC because AB is longer. ProofWiki doesn't mention this, but I think it's a nice addition to the proof. By the way, I have a list of all the titles of your videos, and searching "exterior" only returned "What is an Exterior Angle?" which you've already linked to. Thus, I'm pretty sure you don't have a video on the exterior angle theorem.

mike_the_tutor
Автор

Thank you much! I hope you are fine.
These videos are cool. Thanks so much!

aashsyed