filmov
tv
the subtleties of sequences of functions

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
the subtleties of sequences of functions
Sequences - Convergence
Calculus I: Examples of Sequence Questions (With Induction!)
Quick Precalc #23: Subtleties with limits and geometrically visualizing limits (of sequences).
Lec 66 - Basic Analysis : Convergence of sequence of functions
Calculus 2 -- Sequences -- Overview
4.1: How to determine if a sequence converges | Wellesley College Calc. 2
Sequences, On-Sequences and Clips | Algebraic Calculus One | Wild Egg
1 - Love Call of the Divine
Power Series | Determining endpoints of the interval of convergence
In Praise of Subtle Cinematography
Series
Real Analysis Course #18 - Sequence Limits are Unique Proof
Sequences, Series, and Convergence - Calculus II (full course) - lecture 23b (of 30)
Can programmers do math? What is a real number, really?
Lecture 11.1: b. The subtlety of bias — [Probability | Santosh S. Venkatesh]
Calculus II, Lecture 14: Sequences
(5.2.29) Deciphering an Alternating Geometric Series: From Summation to Closed Form
Challenges with higher on-sequences | Real numbers and limits Math Foundations 101 | N J Wildberger
Sequences: examples and notation
The successor-limit hierarchy and ordinals I Data structures in Mathematics Math Foundations 181
Sequences and Series
ECE 260 --- Preliminaries --- Functions, Sequences, System Operators, and Transforms
Kit Cambridge, 'EcmaScript Next: The Subtleties of ES 6' at W3Conf 2013
Комментарии
 0:17:36
0:17:36
 0:21:08
0:21:08
 0:32:04
0:32:04
 0:13:00
0:13:00
 0:59:30
0:59:30
 0:29:46
0:29:46
 0:15:03
0:15:03
 0:34:31
0:34:31
 1:08:39
1:08:39
 0:09:06
0:09:06
 0:14:01
0:14:01
 0:23:45
0:23:45
 0:05:35
0:05:35
 1:05:25
1:05:25
 0:10:13
0:10:13
 0:17:59
0:17:59
 0:25:15
0:25:15
 0:02:27
0:02:27
 0:35:32
0:35:32
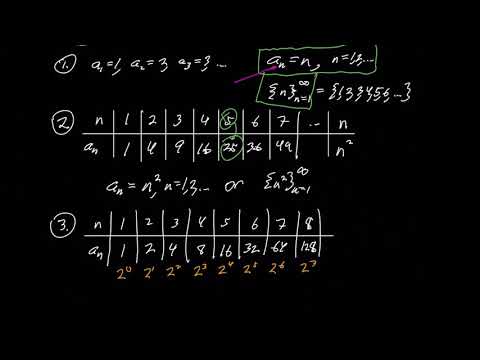 0:17:17
0:17:17
 0:21:52
0:21:52
 0:06:50
0:06:50
 0:33:34
0:33:34
 0:41:58
0:41:58