Marek Filakovský: Embeddings and Tverberg-Type Problems: New Algorithms and Undecidability Results

Title: Embeddings and Tverberg-Type Problems: New Algorithms and Undecidability Results

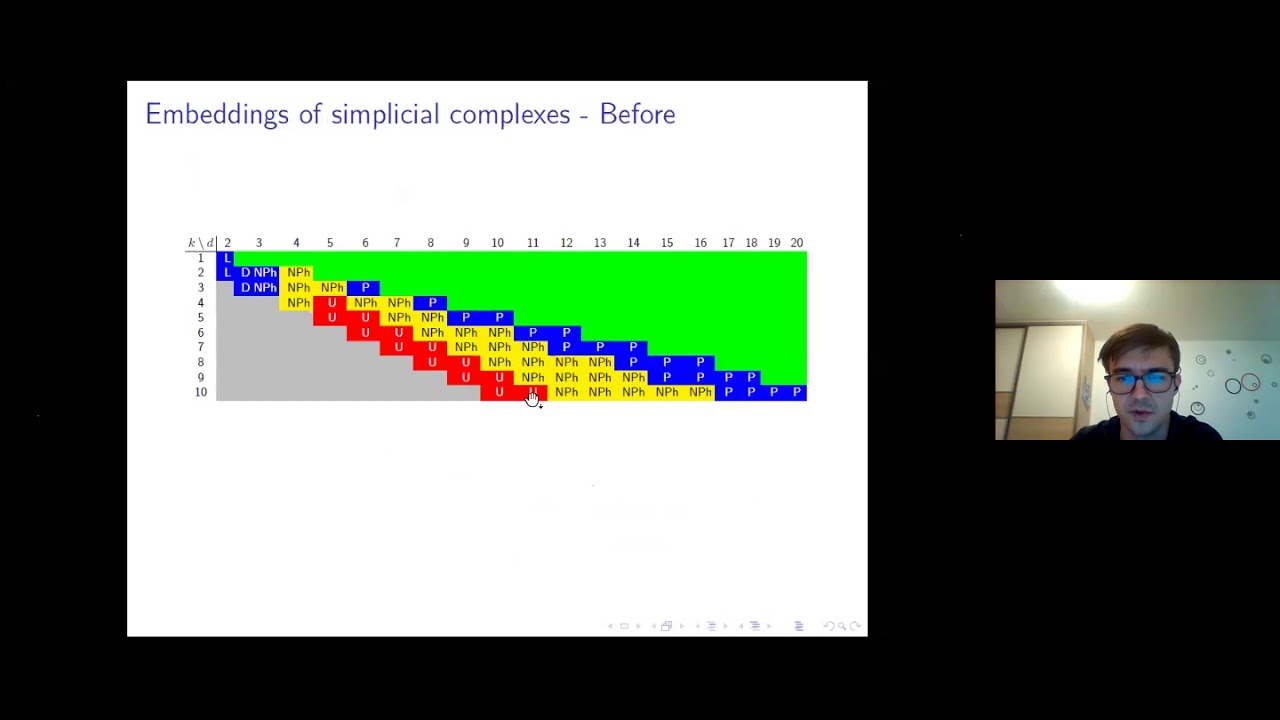
Abstract: We present two new results in computational topology. The first result, joint with Uli Wagner and Stephan Zhechev, concerns the algorithmic embeddability problem, i.e. given a k-dimensional simplicial complex K, does there exist a (piecewise-linear) embedding of K into d - dimensional Euclidean space R^d? We show that for a wide range of dimensions the problem is algorithmically undecidable. This hints at a sharp dichotomy between polynomial-time decidability and undecidability of the problem in higher dimensions.

The second result deals with a generalization of the embeddability problem called r-Tverberg problem. Here, we ask whether there exists a (piecewise-linear) map f from K to R^d such that no point f(x) has preimages in r distinct pairwise-disjoint simplices. In a joint work with Lukas Vokrinek, we show that r-Tverberg problem is polynomial-time decidable in the metastable range of dimensions (rd greater than (r+1)k + 2).