Generate All Palindromic Decompositions Of A String ('Palindrome Partitioning' on Leetcode)

📹 Intuitive Video Explanations
🏃 Run Code As You Learn
💾 Save Progress
❓New Unseen Questions
🔎 Get All Solutions

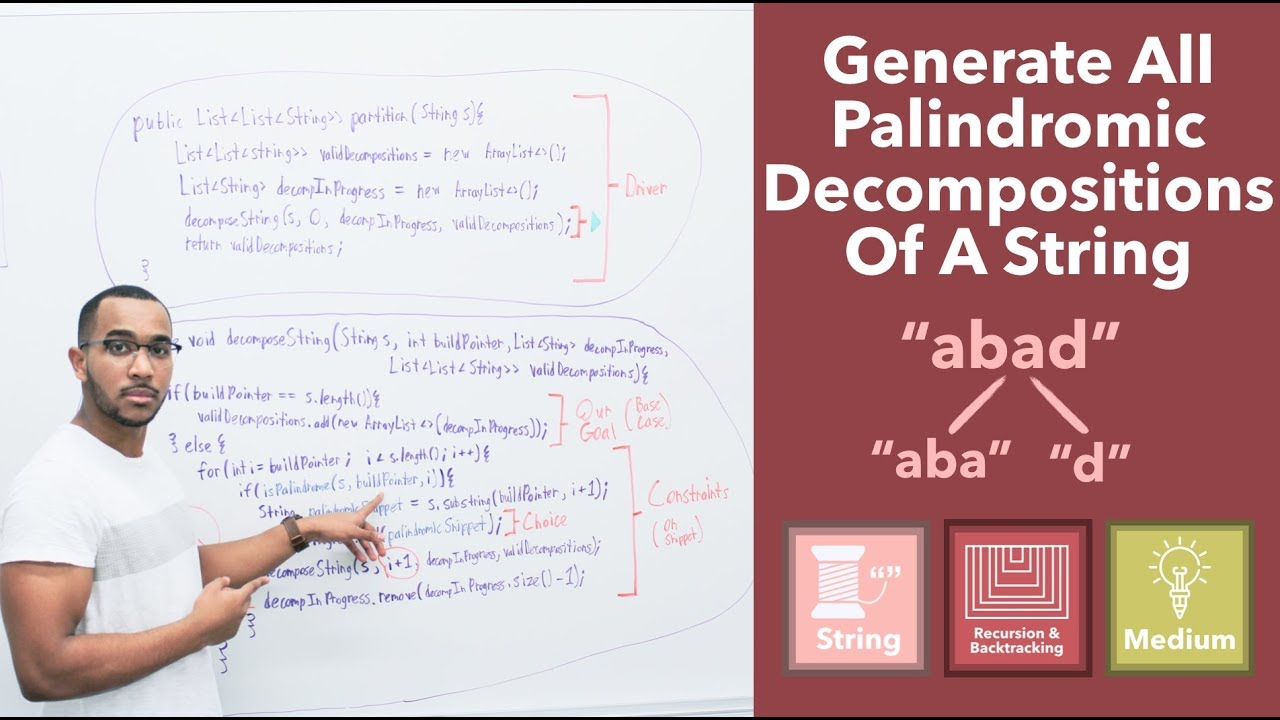
Question: Given a string, return all decompositions of the string that consist of only palindromes.

Example:

Input: "aab"
Output: [ ["aa","b"], ["a","a","b"] ]

Why is this problem backtracking?

It is backtracking because we will be expressing all of the possibilities of a search space given constraints. When we need to represent many decisions and possibilities, backtracking is the tool you should pull from your pocket.

Approach 1

Generate all decompositions and then only add the palindromic decompositions to our answer.

This is highly exponential in time since there are 2^(n - 1) palindromic decompositions.

This wastes a lot of time since we will continue to build on a decomposition that immediately disqualifies as palindromic.

Approach 2

We will take "snapshots" of snippets as we advance through the string and see if they can add to the decomposition that we want to build.

The 3 Keys To Backtracking:

Our Choice

The start and the end of a "snapshot" that we want to add to a decomposition we are working on.

Our Constraints

Each piece of the decomposition must be a palindrome, we cannot choose and advance on a non-palindrome snippet.

Our Goal

Decompose the whole string. When our decomposition progress index is the length of the array then we know that we have achieved this.

Complexities

Time: O(n * (2^n))

Worst case, but much better than approach 1 since this is a rare worst case where all decompositions turn out to be palindromic (a string of all 1 character).

Our best case becomes greatly improved.

We are basically taking subsets so (2^n) and the O(n) time to copy array to our answer.

Space: O(n)

At worst we will always go n stack frames deep in our recursion since an all single character decomposition is always a palindromic decomposition. This does not include the output array in space.

But let us imagine that we do include the output space.

We will have (2 ^ (n-1)) decompositions of the string.

We will certainly not have (2^n) PALINDROMIC decompositions for the string in a normal case.

The length of each decomposition will very likely not be n in the normal case (n/2 is probably a better approximation but I'm honestly not sure).

So approximate length for each decomposition: (n/2).
MAXIMUM decompositions we could ever make: (2 ^ (n-1)).

So this yields a VERY loose upper bound on the space with the output array included:

O( (n/2) * (2 ^ (n-1)) ) = O( n * 2^n)

REMEMBER THAT n IS THE # OF CHARACTERS IN THE STRING PASSED IN TO US.

I just want to get you thinking about this, it is all about demonstrating that you can think along the right lines and get back on track whether you are exactly right or not.

++++++++++++++++++++++++++++++++++++++++++++++++++

++++++++++++++++++++++++++++++++++++++++++++++++++

This question is number 16.7 in "Elements of Programming Interviews" by Adnan Aziz, Tsung-Hsien Lee, and Amit Prakash.

[BackToBackSWE]

Table of Contents: (I'm shouting in this vid, my bad, didn't have a mic way back when)

The Leetcode Dream Continues 0:00 - 0:04
A Quick Message About Patterns Between Problems 0:04 - 0:59
The Problem Introduction 0:59 - 2:43
The Approaches (3 Keys To Backtracking) 2:43 - 5:22
Code Walkthrough 5:22 - 9:10
Time Complexity 9:10 - 10:12
Space Complexity 10:12 - 10:54
Subscriber Harvesting 10:54 - 11:36

The code is in the description (heavily commented for teaching purposes). I'm literally shouting in this smh...my bad.

Note:

all decompositions of a string ≠ all the sub-strings of a string

The number of substrings of a string is n(n+1)/2. There are 2^(n-1) decompositions of a string (no constraints on how we decompose the string, we just break the string up however we choose as long as we exhaust all possibilities).

Example:

n = 3
"abc"

Substrings: (3)((3)+1)/2 = 6
[ "a", "b", "c", "ab", "bc", "abc" ]

Decompositions: 2^((3)-1) = 4
[ [ "a", "b", "c" ], [ "a", "bc" ], [ "ab", "c"], [ "abc" ] ]

...wait...why 2^(n-1) decompositions. Well an intuitive explanation is that of CHOICE.

Remember how for a set of size n we have 2^n subsets? This is because for n elements we can do 2 THINGS, choose that element to put it in the final subset, or NOT choose that element to put it in the final subset.

Same principle here except we have 2 choices for n - 1 PARTITION POINTS.

For example:

n = 3
"abc"

I have 2 PARTITION POINTS that I can make 2 choices on: USE IT or DON'T USE IT. So as follows:

"a | b | c"

Do you see those split points?

If I use the first and second I get [ "a", "b", "c"]
If I use just the first I get [ "a", "bc"]
If I use just the second I get [ "ab", "c"]
If I don't use both I get [ "abc"]

I hope this clears it up (and how this does not relate to taking substrings).

[Trails]

This man is preaching leetcode and algorithmic patterns...

Respect

[lifeofbarkin]

I've never seen a more enthusiastic person ever in my life. Keep up the good work, man! Loved your videos.

[Kee]

I have levelled up from zero to being comfortable with coding backtracking questions in just one day by watching your videos. You are doing a great job in making someone understand the intuition behind these backtracking problems.

[sarakeshtic]

I have a Google interview in 3 days and nothing has taught me more in last one month than you and geeksforgeeks.

[najimali]

Hey, the explanation is not so good, Although I understood it from your explanation.;
Suggestion - instead of showing code, you can draw a recursion tree for the same example & explain it that would be more helpful.
If a person can imagine the flow then writing the code is not a big deal for him.

[srujanbelde]

I liked your video because you have not just explained the solution but the basic idea of it, This helped me analyze problems from a different perspective. Thanks! :)

[iamnoob]

I did not understand completely, But when i traced the code which u have provided in github, I understood it completely.Your channel is one of the best channels in youtube for learning Algorithm problems for coding Interviews.Keep posting more videos maybe 2videos/week if possible, It would help us a lot.Thank you

[takanashiouken]

Thank you so much. I couldn’t understand the explanation on leetcode, but you explain makes things clear.

[raghav]

I understand why time complexity is O(n*2^n)
But if we look at code and create recurrence relation we see that
T(n) = 1+T(n-1) + 2+T(n-2) + 3+T(n-3) + 4+T(n-4) + ... + n-1+T(1)

Because for a given in in range(1, len(s)+1), checking the palindrome will take i time and we are calling the recursive function on substring of length n-i

So T(n) = n*(n-1)/2 + T(n-1) + T(n-2) + T(n-3) + T(n-4)...+T(1)
T(n) = O(n^2)+ T(n-1) + T(n-2) + T(n-3) + T(n-4)...+T(1)
How do we calculate T(n) from here?

[DarkKnightUNS]

this video is the Great suppelment of EPI+Leetcode. Thanks

[Hello-jnsk]

Sir You are one of the best YouTuber for CP that i have seen, please keep your brilliant work up and make more videos on some standard questions of DSA.

[biikaaa.]

i can't solve any medium recursion questions without these videos, i feel so bad

[kunpeng]

pattens..., what a great idea, you create and deliver the most crucial part of programming, so appreciate your effort!

[pardeepsharma]

Don't listen to your Haters. Keep doing, you are Awesome :)

[yizhihu]

Great video. A question: Why is the number of decomposition is 2^n. For example, if we have abcde, we can decompose them into 1 char which has 5 decompositions, 2 chars which has 4 decomposition, 3 chars which has 3 decomposition, 4 chars which has 2 decomposition and 5 chars which has 1 decomposition. So add them all up, we have 1+2+3+4+5 = 15 decomposition, which looks like a (n-1)^2 instead of 2^n

[frazikram]

I might just not be seeing it but where the link to the github for this problem?

[pragyavyas]

Enthusiastic, it takes me to the pattern present everywhere.

[gauravshahare]

Hi thank you very much only after this video i understand how to calculate the time and space complexity of backtracking algorithm

[arnobchowdhury]

I wish you could see my the frequency head nodding I do while learning from your videos.