Friction (Assignment)

#Assignment
#Friction
#Physics
#AKYSir
Q1. What is the unit of coefficient of friction
Q2. Name the factor on which coefficient of friction depends?
Q3. Friction is a self adjusting force. Justify.
Q4. Figure shows a man standing stationary w.r.t a horizontal conveyor belt that is accelerating with 1 m s-2. What is the net force on the man? If the coefficient of static friction between the man’s shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt? (Mass of the man = 65 kg.)
Q5. A small block of weight 12N is at rest on a smooth plane inclined at 40o to the horizontal. The block is held in equilibrium by a force of magnitude P. Find the value of P when
(i) force is parallel to the plane
(ii) force is horizontal
Q6. A block of mass 10kg is sliding on a surface inclined at an angle of 30o with the horizontal. Calculate the acceleration of the block. Coefficient of kinetic friction between the block and the surface is 0.5.
Q7. A block of mass 15 kg is placed on a long trolley. The coefficient of static friction between the block and the trolley is 0.18. The trolley accelerates from rest with 0.5 m s-2 for 20 s and then moves with uniform velocity. Discuss the motion of the block as viewed by
(a) a stationary observer on the ground, (b) an observer moving with the trolley.
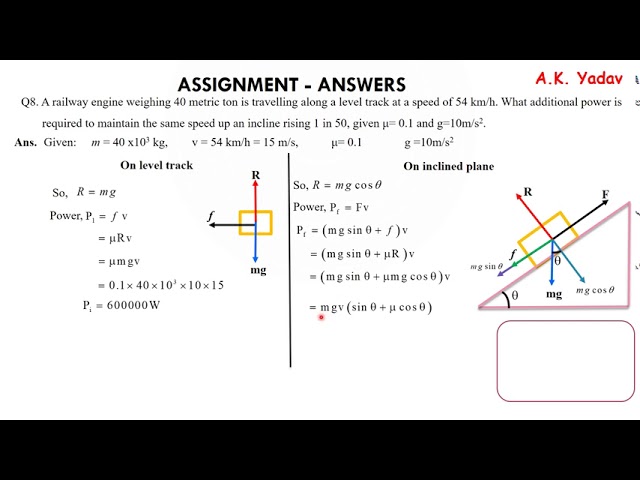
Q8. A railway engine weighing 40 metric ton is travelling along a level track at a speed of 54 km/h. What additional power is required to maintain the same speed up an incline rising 1 in 50, given μ= 0.1 and g=10m/s2.
Q9. Two blocks connected by an inextensible string passing over a light frictionless pulley are resting on two smooth inclined planes as shown. Determine the acceleration of the blocks and the tension in the string. Assume string massless
Q10. Two bodies A and B of masses 5 kg and 10 kg in contact with each other rest on a table against a rigid wall. The coefficient of friction between the bodies and the table is 0.15. A force of 200 N is applied horizontally to A. What are (a) the reaction of the partition (b) the action-reaction forces between A and B ? What happens when the wall is removed? Does the answer to (b) change, when the bodies are in motion? Ignore the difference between μs and μk
Q11. Two blocks each having mass 20kg, rest on a frictionless surface as shown. Assuming the pulleys to be light and frictionless, calculate
(a) acceleration of the system
(b) tension in the string
(c) time required for block A to move 1m down the plane.
Q12. (a) Two identical boxes, each of mass 400kg, are at rest, with one on the top of the other on the horizontal ground. A horizontal force of magnitude P is applied to the lower box. The coefficient of friction between the lower box and the ground is 0.75 & the coefficient of friction between the boxes is 0.4. Show that the boxes will remain at rest if P ≤6000.
(b) The boxes start to move with the acceleration ‘a’. Given that no sliding takes place between the boxes, show that a ≤ 4 and deduce the maximum possible value of P.