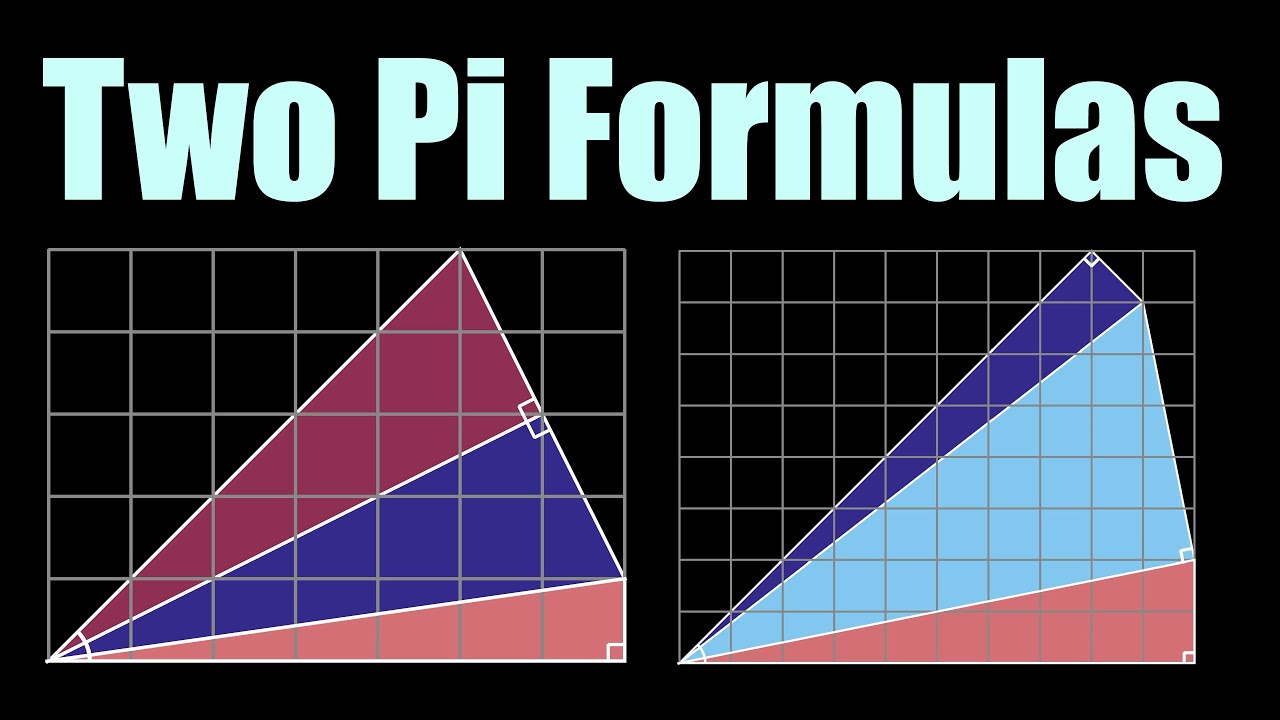
Two Amazing Machin-like Formulas for Pi/4 (Pi Approximation Day Visual Proofs)

This video describes a relatively new visual proof of two different Machin-like formulas for Pi (or for Pi/4 more accurately), which is a formula that allows for relatively speedy computation of the digits of Pi. These two formulas are called Hutton's formula and Strassnitzky's formula although at least Hutton's was likely known to Machin.

#mathvideo math #pi #piday #geometry #inscribed #circumscribed #triangle #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #similartriangles #mathvideo #machinformula #machintheorem #digitsofpi #trapezoid

Here are three more Pi day gems:

To learn more about animating with manim, check out:
____________________________________________________
Background music:
Frozen in Love by Aakash Gandhi

[RandyKing]

nice! the animation makes it simple enough that a child could understand it…and then hopefully start thinking mathematically with various representations and follow their curiosity

[thomasolson]

That's the Fibonacci one. You can continue it.

Notice we are missing 1/3 and 1/5 and 1/8 are consecutive. We kill 1/8 and replace it with 1/13 and 1/21


I think there is a way to get the even terms but I don't remember. Maybe alternate sign? This can be applied to all quadratic type recursive numbers, or at the very least the metalic means ratios. It probably has something to do with some sort of derivative or integral. I don't know enough about those yet.

[TrangNguyen-jtcd]

this channel is answering the real needs !!!! +1 supporter!

[Ninja]

Could you do a video to prove the one that goes


I’ve seen it in matt parker’s video and he mentioned that it was used in the 1800s to calculate pi to over 500 digits. But i was wondering where the formula came from.

[Discovery.specimen]

Bro what is your qualification in math I want to do the same

[kextrz]

Among the numerous ways to calculate π, I don't get the point of using any formula based on reversed trigonometric functions, since those formulas produce results that are angles. π is an angle. Simply doing arctan(1), or either arcsin or arccosin(√0.5) results as 1/4π. What's the point of having π handed to you by simply pushing a few buttons?

[imperfectclark]

Can we get an animation about the following series:

pi ≈ (4/1) - (4/3) + (4/5) - (4/7) + (4/9) ...

It's elegant, though I imagine there are pi approximation algorithms that converge more rapidly.

[BillGreenAZ]

I'll bet there are several other similar ratios of sides that would fit this pi/4. And then there must be similar number of squares to prove other fractions with pi as the numerator.

[orterves]

To a layman like me those "arctan" might as well be "arcane" - it's a whole blackbox of magic

Can these be further decomposed to explain arctan as something more primitive?

[omnipotentfish]

Why not draw a single right angle triangle with angles π/3, π/6, π/2 and then you get tan(π/3)=sqrt(3)
Therefore π/3 =atan(sqrt(3)), finally
π=3•atan(sqrt(3)).
This is much simpler and you need only one triangle.

[MichaelRothwell]

Here is curious fact:

π/4=∑(n=1 to ∞) arctan(1/F₂ₙ)

where Fₙ is the nth term of the Fibonacci sequence.

For a proof, see my (first) reply to the comment by @thomasolson7447, which generalises the 2nd formula,
π/4=arctan(1/2)+arctan(1/5)+arctan(1/8),
which is the sum of the arctans of the reciprocals of certain Fibonacci numbers.

[GourangaPL]

the main question is: "So what?" How can we use this?