Standardizing Normally Distributed Random Variables

I discuss standardizing normally distributed random variables (turning variables with a normal distribution into something that has a standard normal distribution). I work through an example of a probability calculation, and an example of finding a percentile of the distribution. It is assumed that you can find values from the standard normal distribution, using either a table or a computer.

The mean and variance of adult female heights in the US is estimated from data found in a National Health Statistics Report:

McDowell MA, Fryar CD, Ogden CL, Flegal KM. Anthropometric reference data for children and adults: United States, 2003-2006. National health statistics re- ports; no 10. Hyattsville, MD: National Center for Health Statistics. 2008.

For those using R, here is the R code for the examples used in this video:

American female heights example (approximately normally distributed with a mean of 162.2 and a standard deviation of 6.8).

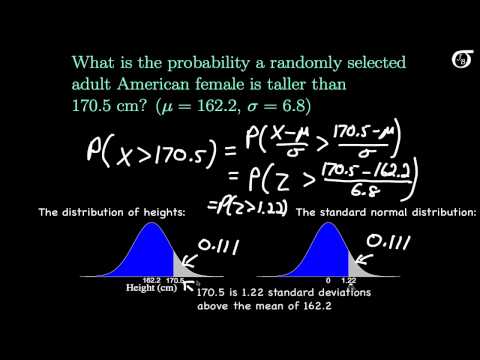
Finding the probability that a randomly selected female is taller than 170.5 cm.
Easiest way:
1-pnorm(170.5,162.2,6.8)
[1] 0.111121

Standardizing route:
1-pnorm((170.5-162.2)/6.8,0,1)
[1] 0.111121
The default in R's pnorm is the standard normal distribution (mean=0, SD=1), so the mean and SD can be left out when dealing with the standard normal.
1-pnorm((170.5-162.2)/6.8)
[1] 0.111121

Finding the probability that a randomly selected female has a height between 150.5 and 170.5.
Easiest way:
pnorm(170.5,162.2,6.8)-pnorm(150.5,162.2,6.8)
[1] 0.8462162

Standardizing route:
pnorm((170.5-162.2)/6.8)-pnorm((150.5-162.2)/6.8)
[1] 0.8462162

10th percentile of heights of adult American females.
Easiest:
qnorm(.1,162.2,6.8)
[1] 153.4854

Alternatively, via the standard normal distribution:
qnorm(.1)
[1] -1.281552
That's the 10th percentile of the standard normal distribution. Converting to the distribution of heights,
-1.281552*6.8+162.2
[1] 153.4854

[kingofgirth]

Videos like these.. 4 years old and still saving the lives of students around the world. Good shit.

[davinchow]

Just want to thank you for this even after 7 years

[simeonkarnes]

In fewer than 3 days of taking notes from your videos, I finally understood what I couldn't figure out in more than 10 days of classes. I got a 96% on my first exam thanks to your videos, and the more I watch the more I understand. Thank you, sir.

[georgiteofilov]

even 10 years later, you're still saving people from failing their exams last-minute :D

[MORamalho]

Hey I just stopped by to tell you how good professor you are!
Thanks for making those videos. Just like other comments told you, you are able to explain things that others try and fail and even create more confusion.

Thanks again! Cheers!

[minabotieso]

I am having a really hard time understanding my statistics lectures and these videos are amazing. Better than Khan Academy and everything else I have found.
I have an online exam today so it is nice that these videos are very short. I have to come back when I am doing the homework.

[jorgeh]

Man you are awesome! You just made my life so much easier. I tried so many channels and two different teachers and so far you can explain in 10 minutes what others take hours! Thank you!

[addson]

I usually never comment, but god damn after watching 1 minute of your video I actually understood more than 1 hour of trying to understand my textbook.... you are amazing!

[Anita-ccsc]

of all the videos ive watched today, yours are the best and makes things easier. You're so far the best in explaining these statistics topics😊🤓

[EDO-nqgw]

video of 7 years old and it is saving my life for the statistics exam. Definitely awesome

[icy-spoon]

Standardizing is something I'm running into a lot lately, and I'm curious about something. If I have a variable x and I want to identify outliers, I could standardize and remove anything above +/- 1.96, or whichever cutoff I choose. I wonder, if x is not normally distributed (e.g. are quite skewed), are z-scores no longer valid? I think that because z-scores are calculated using the mean, but since x is not normal, the mean is no longer a reasonable value for this. Is this correct?

[j.o.s.h.o]

you actually saved me. Thank you for explaining this in a digestable manner. I wish I had found you earlier!

[RedRiverChannel]

When I look at 1.22 in the table, I find 0.8888 and NOT 0.111. What is wrong?

[ellybellyshin]

I dont get where did you get 0.846 in q2, I know its from the table but where.. and how..

[valeriereid]

So glad I found this channel. Thanks so much for the step by step explanation. Your video was very helpful.

[ShirinTejani]

Hi, just wanted to confirm, the std. deviation if 6.8 is a value given in the question on 10th percentile calculation. Or is it something that is calculated from somewhere?

[nped]

How would you calculate the probability of the exercise with the adult American female and her height if the equation said P(150.5 < X -10 < 170.5)?

[jbstatistics]

I'm glad you find my videos helpful.

The random variable X has a mean of mu (E(X) = mu). (X-mu) is itself a random variable, with a mean of 0. E(X-mu) = E(X) - E(mu) = mu - mu = 0. As a simple example, suppose we have a distribution with a mean of 3. If we create a new distribution by subtracting 3 from every possible value, then the mean of the new distribution would be 0.

[simonpaisley]

How do you find the -1.28 using software though? (ie. using R). I understand how to get the value from the standard normal table but I don't know the formula in R. Do you know the formula?

[achievementcell]

1. I watched your videos on how to read standard tables but still can not understand how the area got to be 0.111.
I think we should look at the table with positive numbers and that gives an area of 0.8888. The table with negative numbers gives an area of 0.111, as you said in the video, but I do not see why we should look at that table in the first place.

2. In the percentiles section, you have marked 0.1 on the left side of our graph. Left side is for negative values, right? Why should 0.1 not come to the right side?

I would be glad if you could help me.

Great video. Thank you.