Basic concept of Liebmann's iterative process odd and even squares

In this video explained Basic concept of Liebmann's iterative process odd and even squares. This method is in higher engineering mathematics and this is also iterative method.
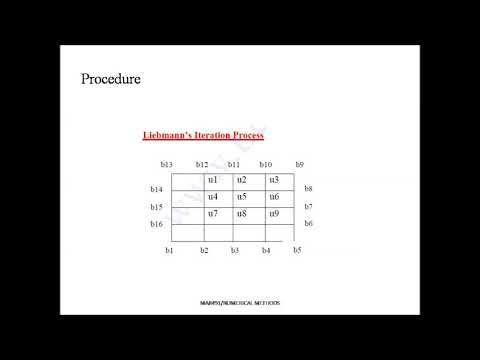
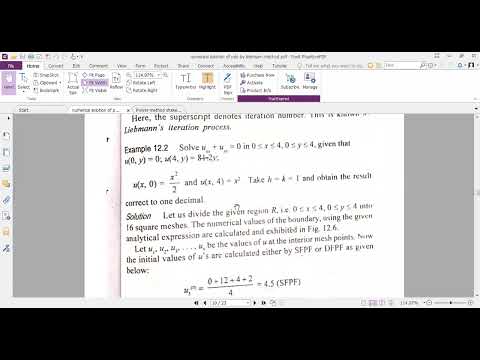
The Liebmann's iterative method also known as the method of odd and even squares is a technique for solving the Laplace equation which is a partial differential equation that describes the distribution of a scalar function (such as temperature or potential) in a two-dimensional region. The basic concept of Liebmann's method is to use an iterative process to update the values of the solution at the grid points where the grid is divided into odd and even squares.

In each iteration the solution values at the odd squares are updated based on the values at the surrounding even squares and vice versa. The process is repeated until the solution converges to a stable value or until a desired accuracy is reached. The idea behind this method is to propagate information from known points (even squares) to unknown points (odd squares) in a systematic manner.

It is important to note that Liebmann's method is a simple and easy-to-implement technique for solving Laplace's equation, but it is not the most efficient or accurate method especially for problems with complex geometries or non-uniform boundary conditions. For more complex problems other numerical methods such as finite difference or finite element may be more appropriate.

LAPLACE TRANSFORM

Fourier Transforms and Z transform

Fourier Series

Calculus of Variation & Numerical Methods

Numerical Methods ODE's

COMPLEX NUMBER

Differential Calculus

Ordinary differential equation

Integral Calculus

Vector differentiation

Differential Calculus & Partial Differential

Joint Probability & Sampling Theory

Probability Distributions

Calculus of Complex Functions

Curve fitting & Statistical Method 1

Linear Algebra

Numerical Methods

#easymathseasytricks #pdesecondorder

Liemann's iteration process for Laplace Equation
iterative method
iterative process flow
what is iterative process
iterative process improvement
general iterative processes
iterative design
iterative methods
iterative model in software engineering
iterative model example
iterative waterfall model

[SSR-eb]

How to improve basic maths sir plzz🙏🙏🙏🙏