filmov
tv
Simplifying | calculator is not allowed #maths

Показать описание
Simplifying | calculator is not allowed #maths
Simplify | calculator is not allowed #maths
Germany l can you simplify this?? l Olympiad Math l Calculator Not Allowed
Simplify | Calculator is not allowed | 9th grade #maths
japanese Olympiad maths questions|| How to simplify|| calculator not allowed||
Calculator Not Allowed | How to simplify?
Casio calculator not displaying a fraction
How to reset the scientific calculator #scintific #calculator
Ukraine l Can you simplify this?? l calculator not allowed l math olympiad
Simplify (2.25)^2.25 l Calculator Not Allowed
Calculator Not Allowed | How to simplify | You should learn this trick
How to solve higher degree equations in casio fx-991ES PLUS
No Calculator! | Can you simplify the radical expression? | Math Rapper
how to convert your calculator in normal mode casio fx-991 es plus (#shorts) #calculator
Indian l can you simplify this?? l Olympiad Math Simplification l Calculator not Allowed
Human Calculator Solves World’s Longest Math Problem #shorts
Questions I get as a human calculator #shorts
How to cheat on test using your calculator #viral #shorts
How to Simplify? | Calculator Not Allowed | Math Olympiad Questions
How to calculate percentage on scientific calculator #scintific #calculator
How to reset a Casio fx-991ES PLUS | Scientific calculator | two way power
How to calculate Percentages?
How To Multiply with Decimals #decimals #multiplication #decimalmultiplication #math #silentmath
How to Simplify? | Calculator Not Allowed | You should know this trick👍
Комментарии
 0:00:37
0:00:37
 0:00:24
0:00:24
 0:08:58
0:08:58
 0:00:44
0:00:44
 0:08:08
0:08:08
 0:05:44
0:05:44
 0:00:25
0:00:25
 0:00:15
0:00:15
 0:08:35
0:08:35
 0:05:33
0:05:33
 0:03:19
0:03:19
 0:00:42
0:00:42
 0:02:27
0:02:27
 0:00:11
0:00:11
 0:07:55
0:07:55
 0:00:34
0:00:34
 0:00:16
0:00:16
 0:00:27
0:00:27
 0:06:24
0:06:24
 0:00:15
0:00:15
 0:00:23
0:00:23
 0:00:16
0:00:16
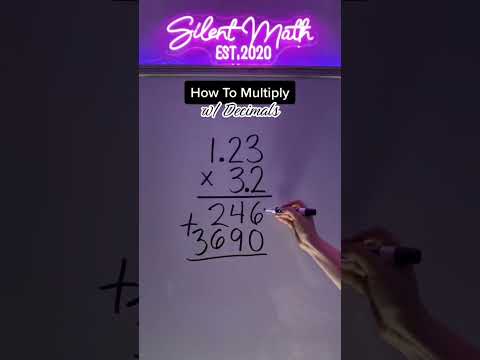 0:00:37
0:00:37
 0:09:11
0:09:11