filmov
tv
Power Series Solution for y'-2y'+y=x, y(0)=0, y'(0)=1

Показать описание
ODEs: Find the first four terms of the power series solution to the IVP y"-2y'+y=x, y(0)=0, y'(0)=1. To check our answer, we find the solution using the annihilator method and expand the exponential terms into power series.
Power Series Solution for y'-2y'+y=x, y(0)=0, y'(0)=1
Power Series Solution of Differential Equation: y'' + x^2y' + xy = 0
Power Series Solution for a differential equation
Power Series Solution of Differential Equation: y'' + x^2y = 0
Solving Differential Equations with Power Series
ODE:: y'' - xy' + 2y=0 :: Power Series Solution about an Ordinary Point
POWER SERIES SOLUTION TO DIFFERENTIAL EQUATION
Power Series Solution of Differential Equation: y'' + xy' +x^2y = 0
Power Series Solution of Differential Equation: y'' - xy' + 2y = 0
Differential Equation Power Series Solution: y'' - x^2y' - y = 0
6.1-18 Find power series solutions of y''+2xy'+2y=0 | DE
Find Two Power Series Solutions for the Differential Equation y'' + xy = 0
6.1-16 Find power series solutions of y''-xy'+2y=0 | DE
Power Series Solution of Differential Equation: y'' + 2xy' + 2y = 0
Power Series - Series Method for Solving Differential Equations - Part 2
How to use SERIES to solve DIFFERENTIAL EQUATIONS example: Airy's Equation y''-xy=0
Find Two Linearly Independent Power Series Solutions to (x - 1)y'' + y' = 0
Series Solution Differential Equations (Example 2)
ODE :: xy'' + y' +2xy = 0 :: Method of Frobenius Series Solution about a Regular Sin...
Ch.6-13 Find power series solutions of y''+xy'+2y=0, y(0)=3, y'(0)=-2 | DE
Use the Power Series Method to solve: y′′ + β^2y = 0
How to solve ODEs with infinite series | Intro & Easiest Example: y'=y
(1-x^2)y''-2xy'+2y =0 solution by Power series II Problem -2
series solutions of y''- xy'- y = 0
Комментарии
 0:06:24
0:06:24
 0:11:59
0:11:59
 0:21:20
0:21:20
 0:12:05
0:12:05
 0:18:29
0:18:29
 0:25:23
0:25:23
 0:37:54
0:37:54
 0:16:47
0:16:47
 0:11:19
0:11:19
 0:11:56
0:11:56
 0:09:37
0:09:37
 0:19:45
0:19:45
 0:12:37
0:12:37
 0:11:12
0:11:12
 0:17:35
0:17:35
 0:13:17
0:13:17
 0:23:29
0:23:29
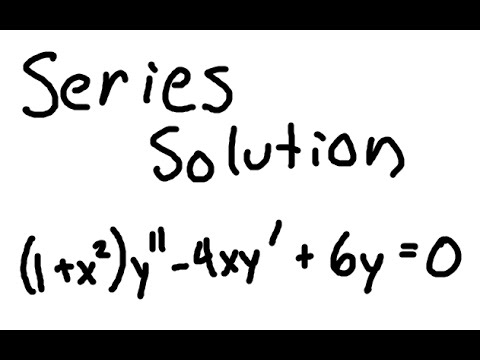 0:30:45
0:30:45
 0:18:46
0:18:46
 0:07:15
0:07:15
 0:07:09
0:07:09
 0:11:01
0:11:01
 0:28:34
0:28:34
 0:19:09
0:19:09