filmov
tv
What is 0 to the power of 0?
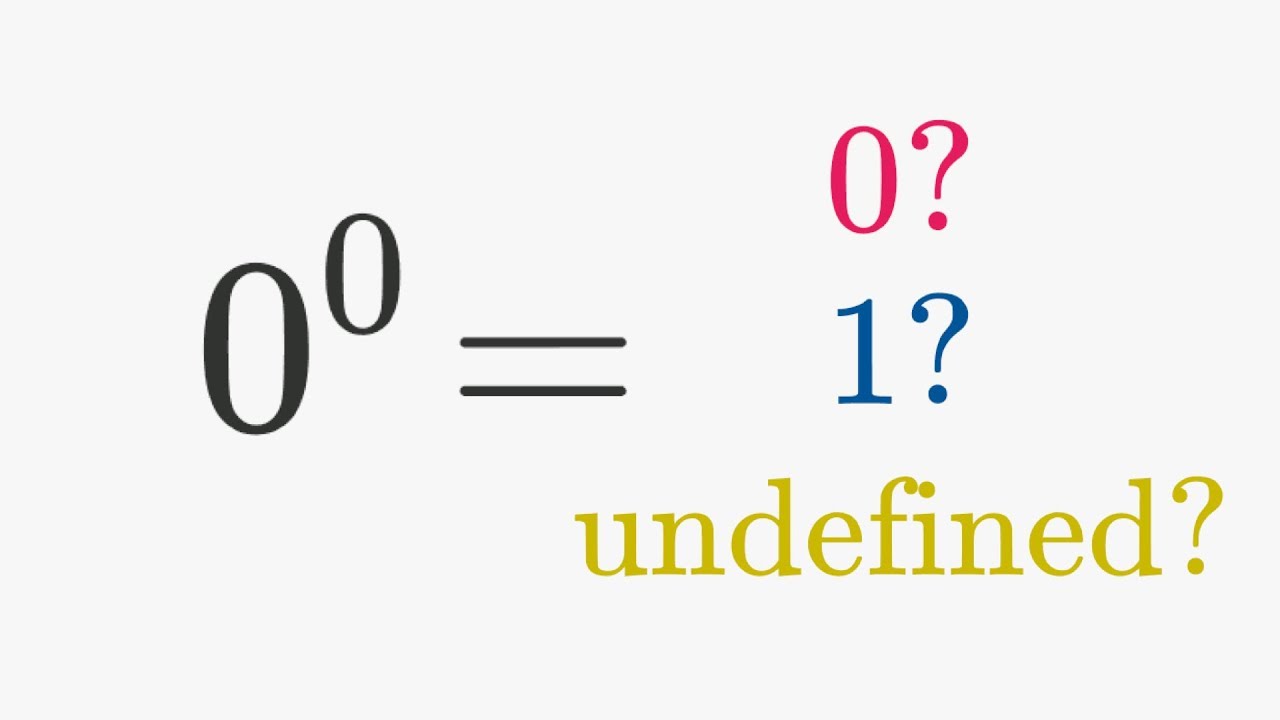
Показать описание
Is zero to the power of zero 0, 1, or undefined? The answer reveals an important idea regarding the nature of math.
Subscribe for weekly math and science videos that'll explore challenging problems, common misconceptions, and intriguing concepts.
FIND US ON:
Subscribe for weekly math and science videos that'll explore challenging problems, common misconceptions, and intriguing concepts.
FIND US ON:
What is 0 to the power of 0?
What is 0 to the power of 0?
What is 0 ÷ 0?
But What Is ∞ ^ 0
What is zero to the power of zero, 0^0, 0 to the power of 0? (using index or exponent laws)
I Finally Found Out What 0/0 Should Be
What is 0^0? (zero-power-zero) | Math Basics | Math2Go
0 ^ ∞ , It's What You Think
0 x ♾️ , It's Not What You Think
Asking Siri what 0 divided by 0 equals.
What Is 0 Divided By 0? Why You Can't Divide By Zero
What is 0 factorial? | Math Basics | Math2Go
What is log 0 =? #shorts #logs #logarithm #math #maths #logarithms #explore #brazillian
what 0 divided by 0 really is
Why 0! = 1? What do you think about the proof? #Shorts #Mathematics
WHAT IS 0 X 0 X 0????
0 degrees celsius+0 degrees celsius =what?!?!?!? #shorts
What if Number 0 (Zero) Disappeared? + more videos | #aumsum #kids #children #education #whatif
what is the value of 0 raise to power 0?
WHAT I USE FOR 0-100 MAKEUP
What If You Stay In Level 0 too long? #backrooms #explained #weirdcore #liminalspace #dreamcore
What Is One Thing Everyone Should Try? | 0-100
The DUMBEST People With 0 IQ
Asking Siri what 0 divided by 0 is *ORIGINAL*
Комментарии
 0:03:25
0:03:25
 0:14:22
0:14:22
 0:00:11
0:00:11
 0:03:29
0:03:29
 0:00:47
0:00:47
 0:04:40
0:04:40
 0:07:57
0:07:57
 0:04:47
0:04:47
 0:05:07
0:05:07
 0:00:25
0:00:25
 0:03:14
0:03:14
 0:05:57
0:05:57
 0:00:09
0:00:09
 0:07:46
0:07:46
 0:00:16
0:00:16
 0:05:05
0:05:05
 0:00:14
0:00:14
 0:03:40
0:03:40
 0:06:11
0:06:11
 0:00:26
0:00:26
 0:00:36
0:00:36
 0:02:24
0:02:24
 0:17:51
0:17:51
 0:00:28
0:00:28