filmov
tv
Awesome Math Party Trick (Three Points on a Colored Line)

Показать описание
Show your friends a fancy math trick: a problem of finding three specially positioned points of the same color on a colored line. Have fun!
Awesome Math Party Trick (Three Points on a Colored Line)
Human Calculator Solves World’s Longest Math Problem #shorts
Read Anyone's Mind With This EASY Math Trick
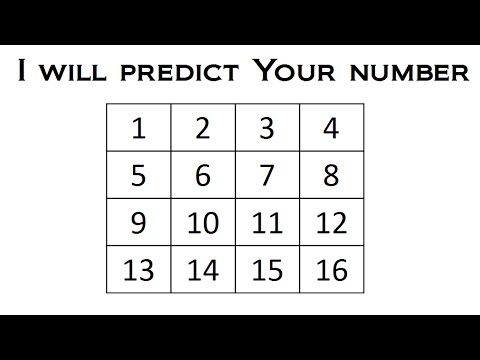
I Will Predict Your Number - Math Magic Trick
party tricks #party #shortsviral #satisfying #mathematics #trending #shortvideos #shorts #trending
Amazing Math magic tricks with Numbers between 0 to10- math magic with numbers - Number magic tricks
Magic tricks||mind blowing #math #trending #shorts
Awesome Math Riddle to Impress Your Friends
Multiplication tricks vedic maths #short #shorts #math #vedicmaths
Cool math trick with a clock! You can easily repeat it! 💥 Cool tricks by BadaBOOM #shorts
[Math Magic] Trick 3: Any Number
Cool math trick #shorts Entertaining math
Magic of 7*11*3 Math Trick #Shortcut #Mathmagic #PWEnglish #Shorts
BUZZ!!! Fun Math Game for the Classroom
MATH TRICKS - A Simple Number Game | This Will Blow Your Friend's Mind
Use this math trick on your friends!
How to solve Math questions ! /Math hacks and tricks by Nan
Mental Math Question Asked To The World's Hottest Math Teacher
Maths puzzle vedic maths #shorts #short #math #vedicmaths
Magic of number 37🔥🔥|| Math tricks || Mathematical champs
2 UNIQUE TRICK TO GUESS AGE (SIMPLE COOL MATH GAMES)
Superb trick! #shorts #shortsvideo #explore #youtubeshorts #triangles #math #geometry #calmdown
Amazing math |math shorts| #Amazing #shorts #mathtricks
15 Easy Magic Tricks to Amaze Your Friends
Комментарии
 0:02:21
0:02:21
 0:00:34
0:00:34
 0:02:45
0:02:45
 0:02:50
0:02:50
 0:00:07
0:00:07
 0:05:13
0:05:13
 0:00:16
0:00:16
 0:01:52
0:01:52
 0:00:06
0:00:06
 0:00:25
0:00:25
![[Math Magic] Trick](https://i.ytimg.com/vi/6kxXslGsQlA/hqdefault.jpg) 0:01:44
0:01:44
 0:00:15
0:00:15
 0:00:49
0:00:49
 0:04:30
0:04:30
 0:03:32
0:03:32
 0:00:57
0:00:57
 0:00:24
0:00:24
 0:03:46
0:03:46
 0:00:06
0:00:06
 0:00:20
0:00:20
 0:03:20
0:03:20
 0:00:10
0:00:10
 0:00:29
0:00:29
 0:14:30
0:14:30