filmov
tv
Proof of p-series convergence criteria | Series | AP Calculus BC | Khan Academy

Показать описание
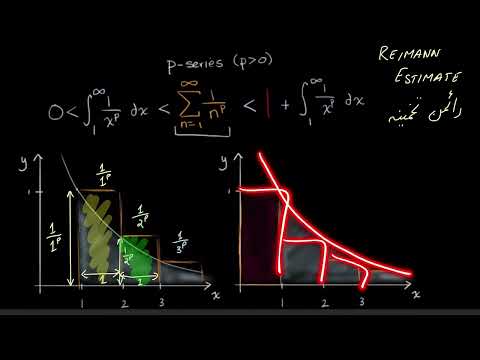
A p-series converges for p "greater than" 1 and diverges for 0.
AP Calculus BC on Khan Academy: Learn AP Calculus BC - everything from AP Calculus AB plus a few extra goodies, such as Taylor series, to prepare you for the AP Test
For free. For everyone. Forever. #YouCanLearnAnything
Proof of p-series convergence criteria | Series | AP Calculus BC | Khan Academy
Proving p series convergence criteria
Series | Lecture 18 | Condition for Convergence of p - series
Proof of p-Series Test
P-Series Introduction and Proof
Choosing Which Convergence Test to Apply to 8 Series
11.3: Proof of the p-Series
Proof of p-series convergence criteria
Proof of p-series convergence criteria
convergence of p series proof using the integral test
P-Series - Proof
The p-Series Convergence Test
P Series test proof | convergence and divergence of a series
P-series
Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test
Session 5 : Integral test with examples and proof of P- Series test.
Proof of p series convergence criteria | Seq Ser | Post Sec Math | KA Urdu
P-series and P-Series Test | Calculus 2
p series test proof|hyper harmonic series test proof
state and prove P-series test
P-Series Test for Infinite Series (Convergence Test)
p series converges if p greater than 1 and diverges if p less or equal to 1. Real Analysis I, Lec-56
Math Tutorial - Series Convergence P-Series
Convergence and Divergence - Introduction to Series
Комментарии
 0:09:36
0:09:36
 0:09:37
0:09:37
 0:12:45
0:12:45
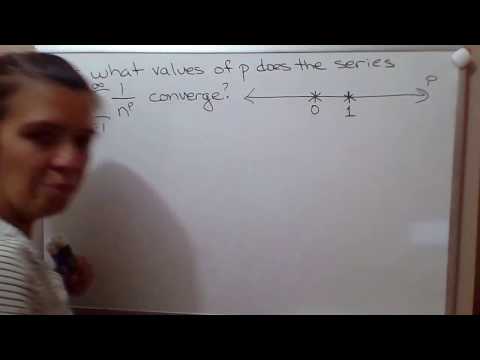 0:10:57
0:10:57
 0:08:40
0:08:40
 0:12:13
0:12:13
 0:09:17
0:09:17
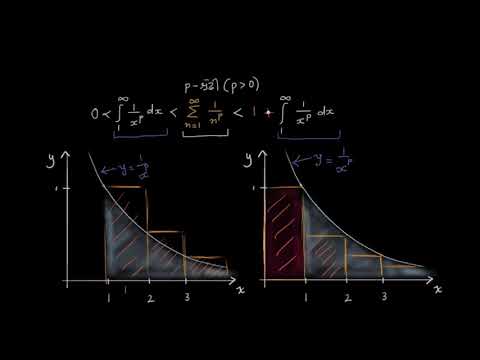 0:09:53
0:09:53
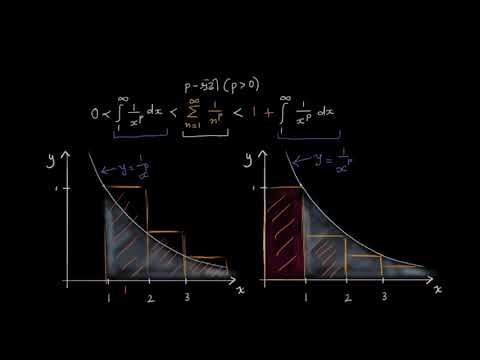 0:09:53
0:09:53
 0:03:42
0:03:42
 0:15:16
0:15:16
 0:04:32
0:04:32
 0:21:49
0:21:49
 0:11:08
0:11:08
 0:43:52
0:43:52
 0:13:12
0:13:12
 0:07:53
0:07:53
 0:09:51
0:09:51
 0:12:33
0:12:33
 0:11:34
0:11:34
 0:10:48
0:10:48
 0:26:05
0:26:05
 0:03:16
0:03:16
 0:16:18
0:16:18