filmov
tv
VOLUMES and polar coordinates: find the volume of the solid under the paraboloid and above the disk.

Показать описание
Use polar coordinates to find the volume of the solid under the paraboloid
z =x^2+ y^2 and above the disk x^2+y^2 less= 9
z =x^2+ y^2 and above the disk x^2+y^2 less= 9
Double Integral to calculate Volume: Polar Coordinates
VOLUMES and polar coordinates: find the volume of the solid under the paraboloid and above the disk.
Finding volume under a surface using double integral in polar coordinates
Finding Area In Polar Coordinates
Calculus 3: Triple Integrals (12 of 25) Finding the Volume Using Cylindrical Coordinates
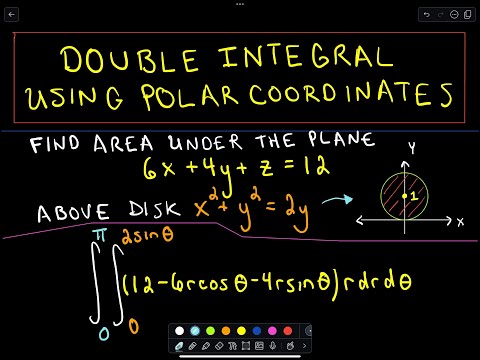
❖ Double Integral Using Polar Coordinates - Part 1 of 3 ❖
Video3211 - Double Integrals - Polar Coordinates - Volume of an Ellipsoid
Volume Elements (dV) in Cartesian, Spherical, and Cylindrical Coordinates
Polar coordinates to find volume inside both the cylinder x^2+y^2=4 and ellipsoid 4x^2+4y^2+z^2=64
Double polar integral to find the volume of the solid (KristaKingMath)
Calculus 3 Lecture 14.3: Double Integrals over POLAR REGIONS
Integration in Spherical Coordinates
Volume of Solid Using Polar Coordinates
Double Integrals in Polar Coordinates
Polar coordinates to find volume inside the sphere x^2+y^2+z^2=16 and outside the cylinder x^2+y^2=4
Physics - Advanced E&M: Ch 1 Math Concepts (26 of 55) Cylindrical Coordinates:Area & Volume ...
Triple Integrals in Cartesian Coordinates | Volume between Surfaces
6 Volume Using Polar Coordinates
Polar coordinates to find volume under cone z=sqrt(x^2+y^2) and above disk x^2+y^2 less than = 9
Polar coordinates to find volume above the cone z=sqrt(x^2+y^2) and below the sphere x^2+y^2+z^2=1
Volumes in Polar: to find the volume of the solid bounded by the paraboloid and the plane z = 1
Triple Integrals in Cylindrical Coordinates
Physics Ch 67.1 Advanced E&M: Review Vectors (76 of 113) Area Element in Spherical Coordinates
How to change the order of integration into polar best and easy example (PART-14)
Комментарии
 0:04:59
0:04:59
 0:04:23
0:04:23
 0:06:09
0:06:09
 0:33:50
0:33:50
 0:04:00
0:04:00
 0:05:16
0:05:16
 0:09:11
0:09:11
 0:06:09
0:06:09
 0:06:01
0:06:01
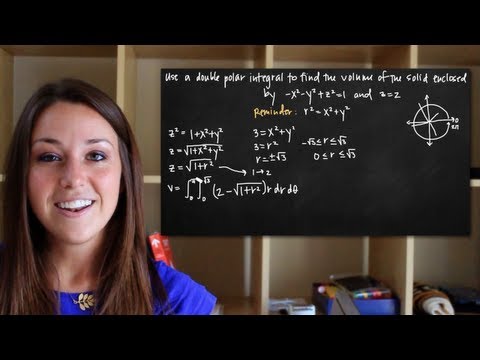 0:12:31
0:12:31
 3:25:15
3:25:15
 0:07:52
0:07:52
 0:03:38
0:03:38
 0:19:48
0:19:48
 0:06:32
0:06:32
 0:02:40
0:02:40
 0:07:13
0:07:13
 0:06:18
0:06:18
 0:03:00
0:03:00
 0:06:53
0:06:53
 0:07:52
0:07:52
 0:20:46
0:20:46
 0:04:09
0:04:09
 0:04:43
0:04:43