filmov
tv
Prove that loga(b)*logb(a)=1
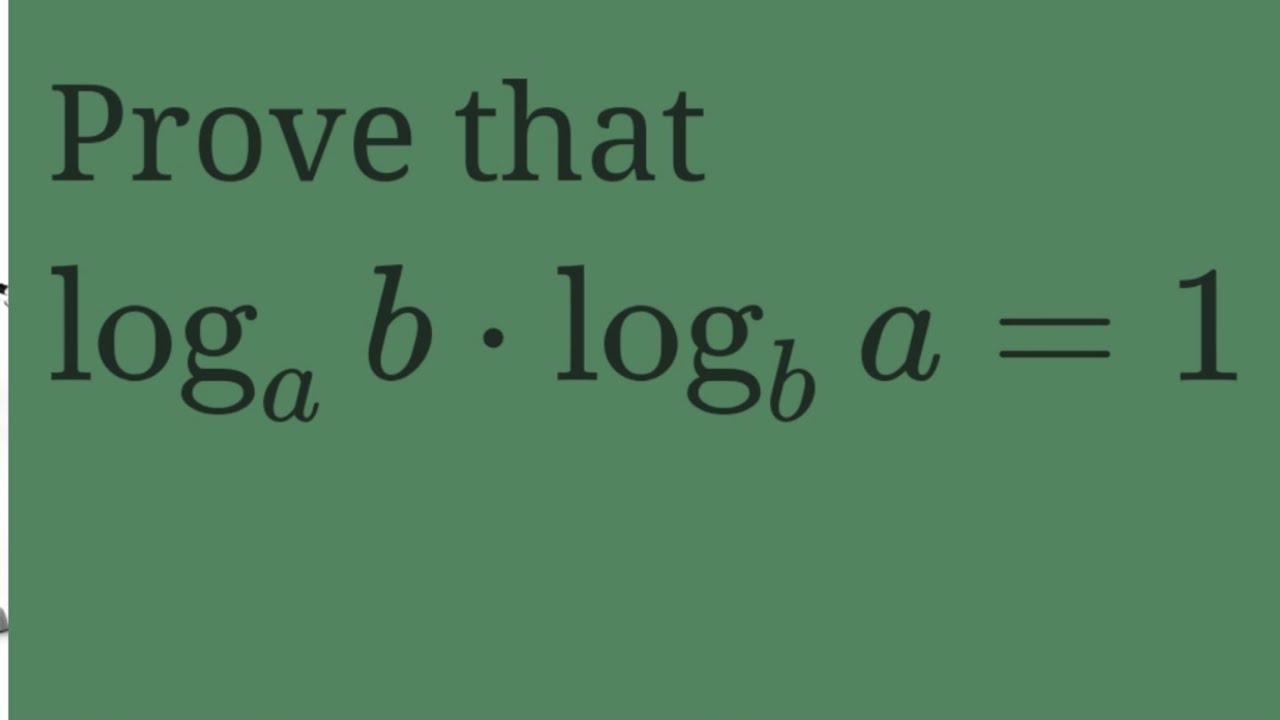
Показать описание
In this YouTube video, we will be discussing the logarithm property. The logarithm property is a mathematical rule that allows us to manipulate equations involving logarithms in order to simplify them or solve for a specific variable. We will delve into the different logarithm properties, including the product property, quotient property, and power property, and show how they can be used to solve various logarithmic equations. Additionally, we will provide examples and practice problems to help you better understand and apply these properties in your own mathematical endeavors. Whether you are a student looking to improve your understanding of logarithms or a teacher looking to refresh your knowledge, this video is sure to be helpful.
Prove that loga(b)*logb(a)=1
Prove logA+logB=logAB
Change of Base Formula Corollary, Logarithmic identities Part 3, log a base b*log b base a=1
Change of Base Formula - Logarithms
Base changing properties of Logarithms (Part 3) : Lecture 7 logab = logcb/logca = 1/logba
Fundamental Properties of Logarithm part 2, Log b base b=1
Logarithms Solved example 1 : log1/3(a+b)=1/2(loga+logb)
Exponential logarithm problem. Prove that a^logb = b^loga
Logarithmic Identities Part 6, b^log a base b = a
loga(b) = 1/logb(a) Proved✅ | #logarithm #log #proved #mathematics
Prove that log_a_(x) = 1 / {log_x_(a)}
log(a/b)=loga-logb || ln(a/b)=lna-lnb Proof of Logarithm Rule
prove that logb^b= 1/ Logarithm proofs/Maths proofs/Basic maths #shorts
log(a/b)=loga - logb proof,loga- logb=log (a/b),prove that log(a/b)=loga- logb,logarithm ,PART-3
06 - Proving the Logarithm (Log) Rules - Understand Logarithm Rules & Laws of Logs
How to show or prove that b to the power of log base b of x = x using logarithms {Show b^log_b(x)=x}
Logarithmic Identity Proof | a^logx b = b^logx a | Step-by-Step Explanation
Log a Base b Times Log b Base c || Logarithm Multiplication Formula || Logarithmic Identities
Prove logA-logB=log(A/B)
Log as Exponent Laws of Logarithms C8
Log 1 base b=0 || Fundamental Properties Of Logarithm Part 1
If log a (b) = log b (c) = log c (a) show a=b=c
Prove that : (1)/( log _(a) ^(abc) )+(1)/(log_(b)^(abc) ) + (1)/( log _c^(abc)) =1 | 9 | CHAPTE...
Base changing property : Solved Example 4 x=1+log(a)bc .. prove that xyz=xy+yz+zx
Комментарии
 0:02:29
0:02:29
 0:01:15
0:01:15
 0:01:43
0:01:43
 0:02:39
0:02:39
 0:03:13
0:03:13
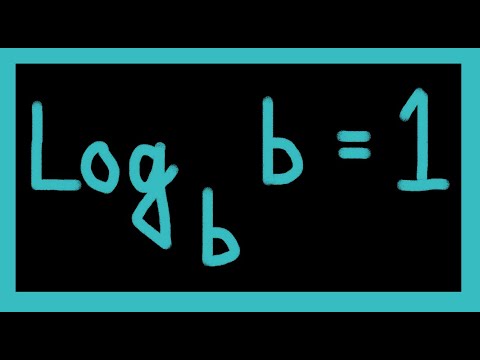 0:00:42
0:00:42
 0:01:21
0:01:21
 0:02:16
0:02:16
 0:00:34
0:00:34
 0:00:36
0:00:36
 0:02:09
0:02:09
 0:01:27
0:01:27
 0:00:26
0:00:26
 0:14:53
0:14:53
 0:16:39
0:16:39
 0:03:06
0:03:06
 0:06:25
0:06:25
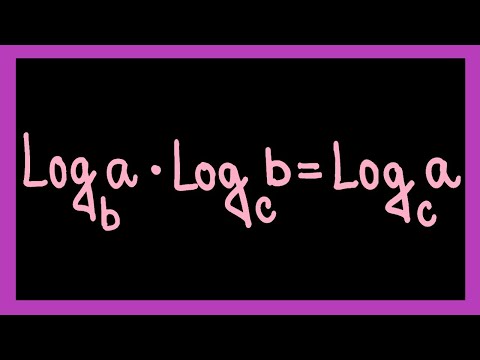 0:01:31
0:01:31
 0:01:15
0:01:15
 0:03:06
0:03:06
 0:00:26
0:00:26
 0:07:12
0:07:12
 0:02:15
0:02:15
 0:01:55
0:01:55