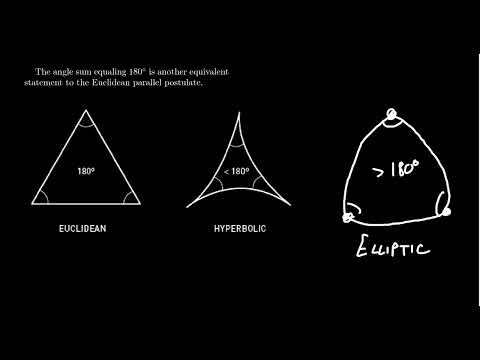
Triangle Sum in Non Euclidean Coordinates

Unit 1: Derivatives for Graphing and Applications (Lectures:25)
The first derivative test for relative extrema, Concavity and inflection points, Second derivative
test for relative extrema, Curve sketching using first and second derivative tests, Limits to infinity
and infinite limits, Graphs with asymptotes, L’Hôpital’s rule; Parametric representation of curves
and tracing of parametric curves (except lines in
3
), Polar coordinates and tracing of curves in
polar coordinates.

Unit 2: Volume and Area of Surfaces (Lectures: 20)
Volumes by slicing disks and method of washers, Volumes by cylindrical shells, Arc length, Arc
length of parametric curves, Area of surface of revolution; Reduction formulae.
Unit 3: Geometry and Vector Calculus (Lectures: 25)
Techniques of sketching conics, Reflection properties of conics, Rotation of axes and second
degree equations, Classification into conics using the discriminant; Introduction to vector
functions and their graphs, Operations with vector-valued functions, Limits and continuity of
vector functions, Differentiation of vector-valued functions, gradient, divergence, curl and their
geometrical interpretation; Spheres, Cylindrical surfaces; Illustrations of graphing standard
theory, geometry, topology and has applications in cryptography, coding theory, quantum
chemistry and physics.
Course Learning Outcomes: The course will enable the students to:
i) Recognize the mathematical objects that are groups, and classify them as abelian, cyclic
and permutation groups etc;
ii) Explain the significance of the notion of cosets, normal subgroups, and of factor groups;
iii) Understand the fundamental concepts of Rings, Fields, Subrings, Integral domains, Vector
spaces over a field, and linear transformations.
Course Contents:
Unit 1: Groups (Lectures: 35)
Definition and examples of groups, Abelian and non-Abelian groups, The group
n
of integers
under addition modulo n and the group
U n( )
of units under multiplication modulo n; Cyclic groups
from sets of numbers, Group of n
th roots of unity, The general linear group; Elementary properties
of groups; Groups of symmetries of (i) an isosceles triangle, (ii) an equilateral triangle, (iii) a
rectangle, and (iv) a square; The permutation group Sym (n), and properties of permutations; Order
of an element, Subgroups and its examples, Subgroup tests, Cyclic subgroup, Center of a group,
Properties of cyclic groups; Cosets and its properties, Lagrange’s theorem, Index of a subgroup;
Definition and examples of normal subgroups.
Unit 2: Rings, Integral Domains and Fields (Lectures: 15)
Definition and examples of rings, Commutative and noncommutative rings, Properties of rings,
Subrings and ideals; Integral domains and fields, Examples of fields:
, , ,
p
and
.
Unit 3: Vector Spaces and Linear Transformations (Lectures: 20)
Definition and examples of vector spaces, Subspaces, Linear independence, Basis and dimension
of a vector space; Linear transformations, Null spaces, Ranges and illustrations of the rank-nullity
theorem.
References curve tracing
polar coordinates polar conversion methof of cubic spline cubic spline explanation graduation 3rd year 2nd year 1st year

[fatitankeris]

If you define straight lines as geodesics in the respective spaces, then all of these are triangles.

[viinisaari]

The surface of a sphere is a non-eucledian space. In that space, it's a triangle, the angles are 90 degreees and the lines are straight.

[the_golden_spiral]

Edit: Have doubts in this video?
I've made full length video with complete explanation. Click on the related video link under the channel name on this shorts.

Hey! I'm Deepak
M.Sc. Maths - IIT Delhi (Currently)
Graduation 🎓 - Kirori Mal College, University Of Delhi
From Haryana, India📍

I love Physics and Maths and upload here the same, the thing that fascinate all us.

•Space
•Physics
•Mathematics
•Engineering

On this planet having approx 7.8 Billion people, only 5.3 B have access to internet, and approx 2B use YouTube regularly, further out of 2 B there are hardly a few millions who like science and have time to watch.

Out of these millions, there is language barrier too, videos can't be made in multi languages 😔 which reduces the numbers to few million or less ( K).

If none of the above things stops you to watch the video on this channel. Then,


Then it's a gentle request to subscribe to the channel so that i can get motivation to upload videos for you and me both 😁


Thank You♥️♥️

[KaliFissure]

You can fit exactly 4 four 360° triangles on the surface of a sphere such that the entire sphere is covered. Which shows also how the surface of a sphere is 4 pi r

[JIT_YT]

I have huge respect for your knowledge but explaining physics from real time cartoon or movie clips is more attractive and applicable.
Also they will give you more views, and physics will also become a part of our life which, in my opinion, is better than theorems and proofs. Thank you IITIAN.

[donovanthompson]

But it is 2 dimensional. You only need two coordinates to describe each point of the triangle. Although you're embedding S2 in R3, it doesn't mean S2 is 3d.

[PushkarPrakash]

Can you provide further proof in long with a proper discussion it seems too easy to dismiss it in a shorts video and if the shape is not a triangle then what is it because its angle are still those of a proper triangle.I'll be really interested in watching a full length video on this topic .Good work 👍

[stevedoetsch]

If you define triangles as squares, then squares can be triangles.

[hanovac]

aren't the lines still straight? at least from some perspectives they are straight.

[RoseRose-yhye]

Can you recommend to me good maths or physics textbooks?

[dev.ocx_]

So we can find out whether we live in a flat universe or not through this experiment 😅