Laplace's Equation on a Rectangle - Partial Differential Equation | Lecture 9

preview_player
Показать описание
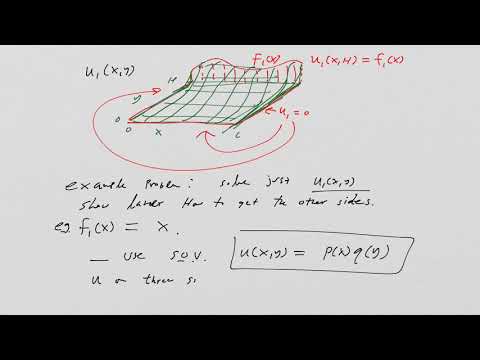
Equilibrium temperature distributions in higher spatial dimensions come from solving a PDE called Laplace's equation. Laplace's equation is difficult to solve in general and its solutions form the basis for harmonic theory. In this lecture we solve Laplace's equation on a rectangle, showing how we can decompose the solution using the principle of superposition and solve each component using separation of variables.

Follow @jbramburger7 on Twitter for updates.
  1. Jason Bramburger
  2. partial
  3. differential equation
  4. derivative
  5. pde
  6. Laplace
Рекомендации по теме
Laplace's Equation on 0:18:07

Laplace's Equation on a Rectangle

Laplace's Equation on 0:20:19

Laplace's Equation on a Rectangle - Partial Differential Equation | Lecture 9

Partial Differential Equation 0:39:45

Partial Differential Equation with Dirichlet Boundary Conditions (With Example)

Solution to Laplace’s 0:33:03

Solution to Laplace’s equation on rectangular domains PART 1

Laplace Equation on 0:18:05

Laplace Equation on a Rectangle, Example #1 [MATH-241] [PDEs]

PDE 101: Separation 0:49:54

PDE 101: Separation of Variables! ...or how I learned to stop worrying and solve Laplace's equa...

Laplace's Equation on 0:18:49

Laplace's Equation on a Rectangle with one Non Zero Boundary Condition

Separation of variables 1:13:27

Separation of variables to solve Laplace's equation for the V in a cube 3D rectangular coordina...

Homogeneous Laplace's Equation 0:19:30

Homogeneous Laplace's Equation on a Rectangle (Part 2)

Laplace Transform of 0:06:27

Laplace Transform of a Piecewise Function (Unit Step Function)

Laplace's Equation (part 0:45:55

Laplace's Equation (part 1): Introduction and Solutions on a Rectangular Domain

V9-9: Laplace Equation 0:21:46

V9-9: Laplace Equation in rectangle, Dirichlet boundary conditions, derivation of formal solution.

Laplace transform of 0:07:07

Laplace transform of unit step function & rectangular window function

Laplace's Equation In 0:11:05

Laplace's Equation In Rectangular Coordinate (Part-1) (Hindi)

Separation of Variables 0:07:10

Separation of Variables - Laplace Eq Part 1

Partial Differential Equations 0:18:02

Partial Differential Equations - 5.9 - Laplace's Equation - Part 1 of 2

ME565 Lecture 10: 0:48:05

ME565 Lecture 10: Analytic Solution to Laplace's Equation in 2D (on rectangle)

Lecture 59 - 0:31:01

Lecture 59 - Laplace equation over a rectangle

Human Calculator Solves 0:00:34

Human Calculator Solves World’s Longest Math Problem #shorts

How REAL Men 0:00:35

How REAL Men Integrate Functions

Working Rule of 0:03:30

Working Rule of solving two dimensional Laplace's Equation,( Rectangle)(Seperation of Variable...

NEWYES Calculator VS 0:00:14

NEWYES Calculator VS Casio calculator

#8. Rectangular Function 0:10:42

#8. Rectangular Function | Laplace Transform | Signals and Systems

mod07lec67 - The 0:28:50

mod07lec67 - The Laplace Equation: Dirichlet and Neumann boundary conditions

Комментарии
Автор

Can we say that as we can solve eigenvalue problem (Lu=lambda×u) in continuous domain when with homogeneous boundary condition, for this reason you take d²(phi)/dy² + lambda×phi = 0 and solve this as at y=0&H, value of phi is zero...?

subhrohalder