S23.2 Poisson Arrivals During an Exponential Interval

preview_player
Показать описание
MIT RES.6-012 Introduction to Probability, Spring 2018
Instructor: John Tsitsiklis

License: Creative Commons BY-NC-SA
  1. MIT OpenCourseWare
  2. Poisson Arrivals
  3. Exponential Interval
Рекомендации по теме
S23.2 Poisson Arrivals 0:09:37

S23.2 Poisson Arrivals During an Exponential Interval

L23.8 Random Incidence 0:04:36

L23.8 Random Incidence in a Non-Poisson Process

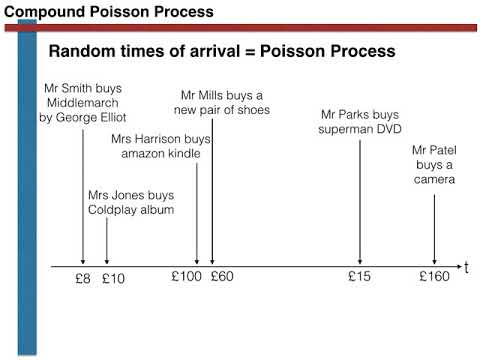
Simulating the compound 0:01:18

Simulating the compound poisson process

L22.2 Definition of 0:05:07

L22.2 Definition of the Poisson Process

L23.2 The Sum 0:04:03

L23.2 The Sum of Independent Poisson Random Variables

Pillai 'Poisson Processes 0:28:36

Pillai 'Poisson Processes and Coupon Collecting'

Pillai: Poisson Arrivals 0:26:22

Pillai: Poisson Arrivals and Departures

Poisson process time 0:09:48

Poisson process time between arrivals

L23.3 Merging Independent 0:08:22

L23.3 Merging Independent Poisson Processes

Introduction to Poisson 0:06:59

Introduction to Poisson Process - Examples

L23.7 Random Incidence 0:09:09

L23.7 Random Incidence in the Poisson Process

Pillai: Next Waiting 0:25:21

Pillai: Next Waiting Time Inference for Random Poisson Arrivals

Probability Pillai 'Poisson 0:09:44

Probability Pillai 'Poisson Processes - Inter-arrival Distributions'

2 Poisson Processes 0:35:43

2 Poisson Processes

SP7 | Poisson 0:09:21

SP7 | Poisson Process | Exponential distribution | Stochastic Processes | Mannan | Arrival

Lecture 10.2: r. 0:09:45

Lecture 10.2: r. Waiting times, the exponential distribution — [Probability | Santosh S. Venkatesh]...

Pillai: Random Selection 0:11:00

Pillai: Random Selection of Poisson Arrivals

Random Processes - 0:12:00

Random Processes - 10 - Poisson Process Properties (Part 2)

SOR1020: The poisson 0:10:02

SOR1020: The poisson process

13-02. Poisson processes 0:32:19

13-02. Poisson processes - Poisson processes and the exponential distribution.

Evaluating a Non-Homogeneous 0:08:01

Evaluating a Non-Homogeneous Poisson Process | MAS 1 Fall 2018 Q2

43 Calculating the 0:09:08

43 Calculating the mean in Inverse Poisson Distribution questions

Pillai: Distribution of 0:09:31

Pillai: Distribution of Departures Between Inter-Arrivals

Exponential + Poisson 0:21:42

Exponential + Poisson = Geometric Distribution!

Комментарии
Автор

Shouldn't the formula be lambda*t at 2:21

fu
Автор

The integral is gamma function, so will integrate to k factorial, and cancel out the k! in the denominator.

魏寅生
Автор

3:05 why isn't it just lambda^k* mu / ( (lambda+mu)* k! ) ?

dlisetteb
Автор

What is the resolution of this exercise:

Consider a queuing model with two attendants and a waiting position operating under steady-state conditions. Suppose that if a customer arrives and finds both agents busy and the waiting position unoccupied, then the customer will wait as long as necessary for service. If the customer finds both attendants busy and the waiting position also occupied, he leaves immediately.

Customers access the system according to a Poisson process with a rate of 2 customers per hour and that service follows an exponential distribution with a mean of 1 hour. The proportion of customers who arrive at the system and will not be served is:

a)2/5 b)1/8 c)2/3 d)2/7 e)1/6

analisecritica