filmov
tv
British Math Olympiad 2012 Problem | Number Theory
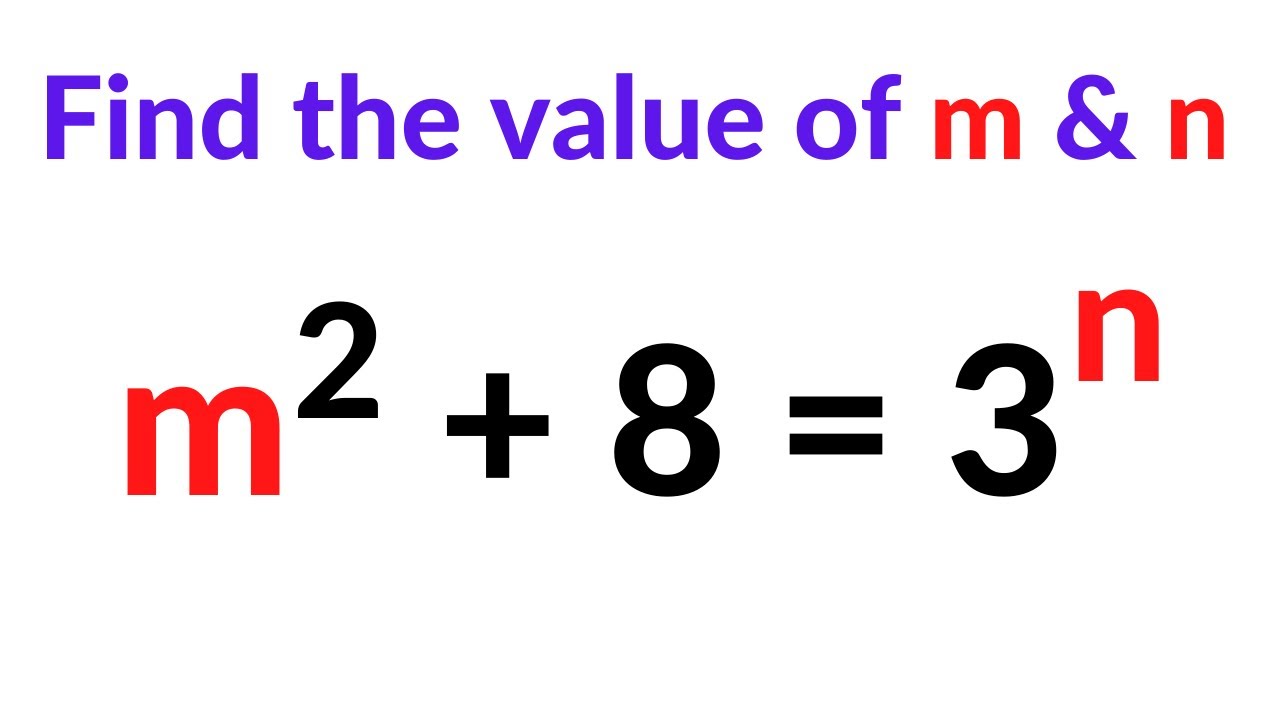
Показать описание
British Math Olympiad 2012 Problem | Number Theory
British Math Olympiad 2012 Problem | Number Theory
British Math Olympiad 2012 Problem | Number Theory
British MOG 2012 Q3 | olympiad number theory problem
A beautiful inequality | International Mathematical Olympiad 2012 Problem 2
A Crazy Inequality under a Bizarre Condition | Turkish Junior Mathematical Olympiad 2012 Problem 3
IMO 2012 - P5
Elegant Powers | Asian Pacific Mathematical Olympiad 2012 Problem 3
A nice problem from the 2012 math olympiad
British Math Olympiad (BMO) Problem 2009
Challenging Algebra Problems (6^2012+ 6^2013)/6^x =7 | Exponential Equation | math Olympiad Problems
Pre Regional Math Olympiad India 2012, Problem 20 | Sine rule of Area | Geometry in Math Olympiad
International Math Olympiad 2012 - Q4: A long functional equation from the IMO
A Big Secret in Solving Number Theory Problems | Turkish Junior Mathematical Olympiad 2012 P1
International Math Olympiad 2012 P1 - A seemingly complex geometry
British Math Olympiad (BMO) Problem 2009
GCD of Polynomials | Number Theory | Korea Junior Math Olympiad 2012 Q4
INMO 2012 - Real Analysis | Sequence of Functions | Maths Olympiad | Problem 3
A Nice Math Olympiad Exponential Equation | How to solve for X in this problem?
British Maths Olympiad Round 2 2005 Q3 | Olympiad Inequality Problems
Number Theory Problem from The Maclaurin Olympiad | Math Olympiad Training
Kyrgyzstan Mathematical Olympiad 2012 | Two Ways to Solve This Functional Equation!
The FIRST Ever IMO Problem
Maths Olympiad Question | Exponential equation | British Olympiad by @MindyourBRAIN1
Problem 6 from the British Maths Olympiad | Inequalities | Math Olympiad Training
Комментарии
 0:05:44
0:05:44
 0:04:08
0:04:08
 0:04:28
0:04:28
 0:11:42
0:11:42
 0:15:29
0:15:29
 0:22:43
0:22:43
 0:22:11
0:22:11
 0:09:32
0:09:32
 0:07:03
0:07:03
 0:03:40
0:03:40
 0:10:51
0:10:51
 0:19:56
0:19:56
 0:06:27
0:06:27
 0:11:52
0:11:52
 0:07:27
0:07:27
 0:11:59
0:11:59
 0:12:59
0:12:59
 0:02:30
0:02:30
 0:04:41
0:04:41
 0:04:08
0:04:08
 0:10:15
0:10:15
 0:00:40
0:00:40
 0:02:44
0:02:44
 0:02:15
0:02:15