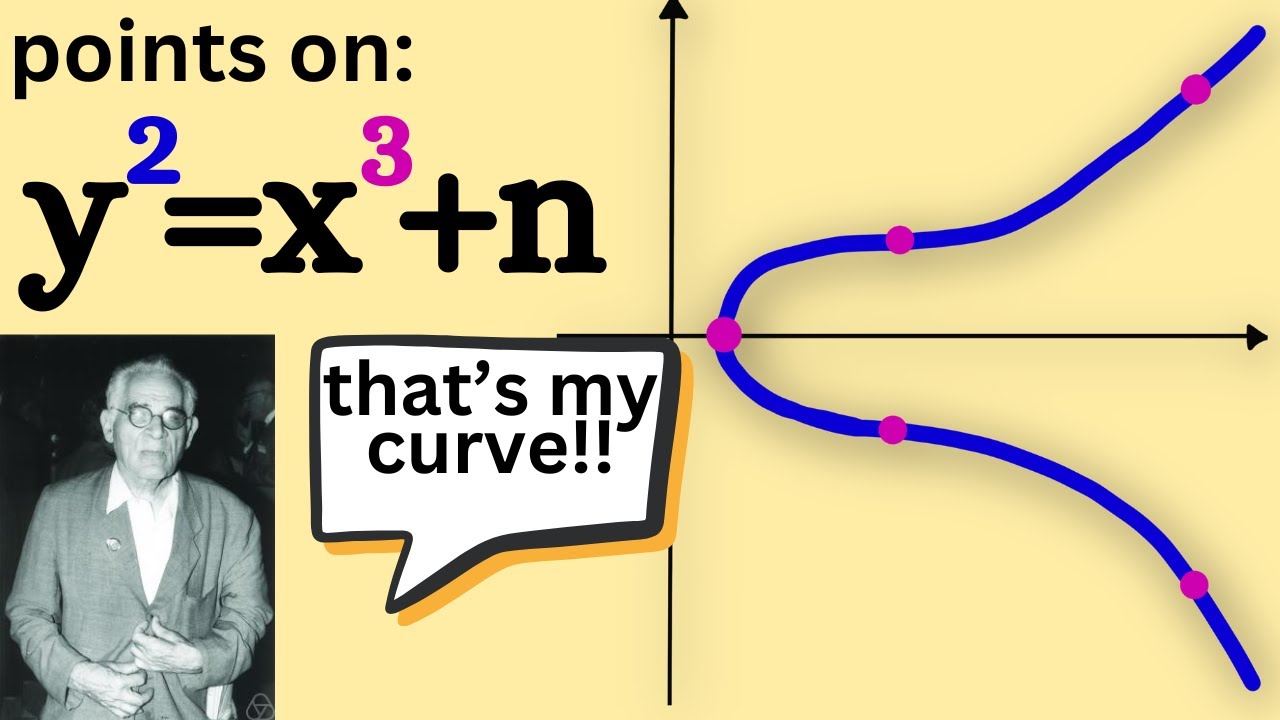
integer points on Mordell curves

🌟Support the channel🌟

🌟my other channels🌟

🌟My Links🌟

🌟How I make Thumbnails🌟

🌟Suggest a problem🌟

[MathFromAlphaToOmega]

When factoring y^2+11 as (y+sqrt(-11))(y-sqrt(-11)), those factors actually won't be relatively prime if y is odd, since then they're each divisible by 2. But then if y is odd, x is even, and then y^2=7(mod 8), which is impossible.

[ikocheratcr]

Nice video as always. Note to editor, please increase video audio volume. Adds on YT play with way higher volume than the video, and when an add plays while you are following along, it is not great to say the least. Makes watching the video a bad experience.

[Alan-zftt]

This video teaches me how much I have still to learn!

[TheRandomFool]

It's pretty trivial to construct Mordell curves with integer solutions. You pick any value of x, and calculate values of n in which x^3 + n produces a square. There are infinitely many Mordell curves that have integer solutions as there are infinitely many squares.

[adamnolte]

At 5:35 there shouldn’t be a cube on the 4a+3… or did I miss something?

[davidbizzozero]

I'm a little late to the chat but doesn't the n=0 case have infinitely many solutions? If x^3 = y^2, then you get (0, 0) and solutions of the form (m^2, ±m^3) such as (1, ±1), (4, ±8), etc. which there are of course infinitely many of.

Edit: nevermind, according the Wikipedia n is a non-zero integer so this doesn't happen.

[viktorgeorgiev]

a²-a=2(mod 8) have 2 solutions 2, 7 but you don't check 7, afterwords that isn't got us a solution for a problem.

[waverod]

Now, as a follow up: is there some pattern or recipe for which values of n give a Mordell curve with (or without) integer points, or is it just happenstance?

[PunmasterSTP]

Mordell curves? More like "Magnificent lecture, that improves"...our knowledge! 👍

[Cat-yztk]

Why is the extension adjoining 1/2(1+sqrt(11)) and not just sqrt(11) also why is it a UFD? Also i know that equations like that have at most finitely many solutions (16 as far as i know) but why? That trick won't work on large numbers where the quadratic extension isn't a UFD

[spkersten]

Why is a^2-a+1 congruent to 1, 3 mod 8 if it has a prime factor like that?

[fartoxedm]

By the way, there are at most 12 integer solutions to an elliptic curve equation

[davidgillies]

Is this anything to do with Birch and Swinnerton-Dyer?

[vikramanbaburaj]

Pretty tough to catch up. Requires a lot of background work.

[Ensign_Cthulhu]

"All odd numbers are of the form 4a + 1 or 4a + 3"... don't you mean 2a+1? And where does 4a+3 come in? Don't 2a+1 and 4a+3 just generate the same number for a different a?

[bentationfunkiloglio]

I apologize for being so immature, but…

that curve perfectly captures my teenage years’ most embarrassing moments!

[fortetwomusic]

I guess it wasn't a good place to stop.

[supratimsantra]

Sir we are so pleased to beyond your imagination....
Thanks a lot from Ramakrishna mission students....from India
Also due respect ❤

[omargaber]

We don't want mordell curve, we want mordell theorem 😎

[omargaber]

Hello Professor Michael, I know that you are a person who only does what your mind tells you and does not listen to the requests of others, but I hope you will accept this request of mine, as I believe that you are the only one capable of that. We need an explanation of the limited gaps between prime numbers by the Chinese Zhang and the French Maynard. We also need an explanation of the scientific paper (Bertrand's Postulate for Carmichael Numbers
Daniel Larsen)
Please do it 😢