filmov
tv
Division algebras and physics (Video 1/14). First video ~ general audience

Показать описание
Note 2: no dividing by zero, of course.
Video 1 of 14 - first video is meant for a general audience
Series: Division algebras and the standard model
Some short videos filmed by Vincent Lavigne
Seminar by C. Furey,
Walter Grant Scott Research Fellow in Physics
Trinity Hall, University of Cambridge
Division algebras and physics (Video 1/14). First video ~ general audience
C. Furey - Division algebras and physics - for a more general audience
Abstract Algebra | Corollaries and examples of the division algorithm for polynomials.
Biquaternions and the Clifford algebra CL(2) (Video 4/14).
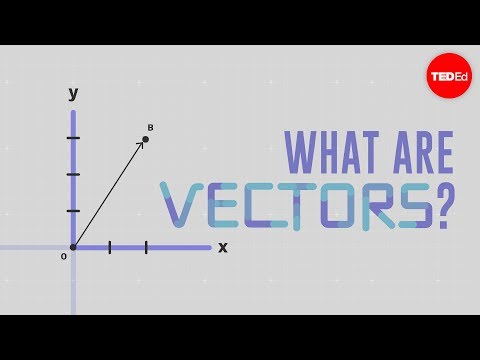
What is a vector? - David Huynh
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
All Of Algebra 1 Explained In 5 Minutes
Nihar Gargava - Lattice packings through division algebras
Quarks and leptons as ideals of the Clifford algebra CL(6) (Video 11/14)
Algebra 1 Basics for Beginners
How to Get Better Grades Without Studying More
Everything You Need to Know About VECTORS
Basic Algebra Tips
How to become a Math Genius.✔️ How do genius people See a math problem! by mathOgenius
Can you solve this? | Exponential Equation | Algebra Problem.
Vectors - Basic Introduction - Physics
Could These Numbers Unravel New Dimensions in Space?
Rules of Fractions in Algebra
Factoring by Grouping Example 😎 #Shorts #algebra #math #maths #mathematics
Algebra For Beginners - Basic Introduction
Algebra Basics: Slope And Distance - Math Antics
Tevian Dray and Corinne Manogue - A Division Algebra Description of the Magic Square, including E8
'GHAPHS PART #1' | maths trick | #maths #mathstricks #algebra #viral #shorts #youtubeshort...
#algebra#equation#easy way#viral#video#how to parts of algebraic equation#song#music#calmdown#
Комментарии
 0:02:02
0:02:02
 0:02:09
0:02:09
 0:17:40
0:17:40
 0:02:54
0:02:54
 0:04:41
0:04:41
 0:00:15
0:00:15
 0:05:00
0:05:00
 0:40:53
0:40:53
 0:08:41
0:08:41
 0:23:05
0:23:05
 0:00:25
0:00:25
 0:17:42
0:17:42
 0:00:48
0:00:48
 0:15:24
0:15:24
 0:03:33
0:03:33
 0:12:13
0:12:13
 0:06:05
0:06:05
 0:01:00
0:01:00
 0:00:27
0:00:27
 0:59:07
0:59:07
 0:12:00
0:12:00
 1:16:11
1:16:11
 0:00:11
0:00:11
 0:00:14
0:00:14