Vertex Colorings and the Chromatic Number of Graphs | Graph Theory

What is a proper vertex coloring of a graph? We'll be introducing graph colorings with examples and related definitions in today's graph theory video lesson!

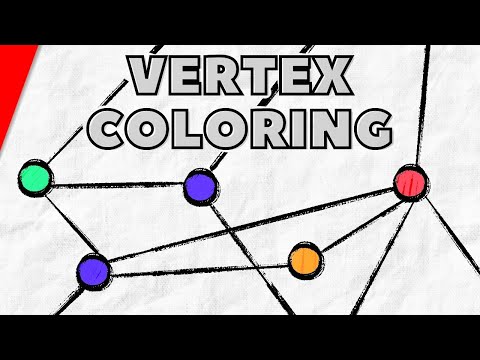
A proper coloring (or just: coloring) of a graph, G, is an assignment of colors (or, more generally, labels) to the vertices of G such that adjacent vertices have different colors (or labels). Consider bipartite graphs for example. If we color all vertices in one partite set blue, and all vertices in the other partite set red, we will have a proper coloring of the graph. None of the red vertices will be adjacent since they're all in a partite set, and similarly for the blue vertices. Furthermore, this means all adjacent vertices will belong to different partite sets and thus have different colors.

The minimum number of colors that a graph G can be colored with is called the chromatic number of the graph, and is denoted χ(G) [this is the greek letter chi, pronounced "kai"]. If χ(G)=k, then G is said to be k-chromatic. If G can be colored with k colors (certainly k is greater than or equal to χ(G)) then G is said to be k-colorable.

A coloring of a graph G using k vertices is called a k-coloring, and if k=χ(G) then it is a minimum coloring, as it uses the minimum possible number of colors. Note that in practice, we often use positive integers (1, 2, 3, ...) to denote our colors. This is far easier than coming up with and using arbitrarily large lists of colors.

Note that every graph of order n can be colored with n colors, since if every vertex has a different color then adjacent vertices will necessarily have different colors. Hence, χ(G) is less than or equal to the order of G.

I hope you find this video helpful, and be sure to ask any questions down in the comments!

********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.

********************************************************************

+WRATH OF MATH+

Follow Wrath of Math on...

[WrathofMath]

NOTE: At 6:30 I describe what it means for a graph to be "k-colorable". The definition I give is common, but not formal enough to avoid some possible confusion. At 7:47 I say a graph cannot be k-colorable for k greater than its number of vertices, since k colors could not be used in a coloring - there simply aren't enough vertices to accommodate k colors if k is greater than the number of vertices. However, this "upper bound" is not common in the usage of the term "k-colorable". Especially as we move on to discussing chromatic polynomials.

Often it may be convenient to say a graph is k-colorable for ANY integer greater than equal to its chromatic number. So while a complete graph on 3 vertices has chromatic number 3, for example, we could say it is k-colorable for any number greater than or equal to 3. Even though we couldn't color it with 10 distinct colors, a set of 10 colors would be sufficient (we just wouldn't use them all), so we may say it is 10-colorable anyways. Always make sure you understand the definitions being used, and I apologize if this causes any confusion!

Support the production of this course by joining Wrath of Math as a Channel Member for exclusive and early videos, original music, and upcoming lecture notes for the graph theory series! Plus your comments will be highlighted for me so it is more likely I'll answer your questions!

[suprecam]

Wonderful video man, thank you. Great explanations, thorough but not too dense, you are easy to understand.

[patriciabalutel]

Hello! Thank you once again for your amazing videos & explanations! Here I am, struggling with two other Graph Theory problems & I was hoping you could enlighten me 😅
First one: show that a planar graph of order n > 2 ( n = number of vertices) contains no more than 3n - 6 edges.
Second one: G is an undirected graph of order n. Show that 𝜒(𝐺)𝜒(𝐺̅) ≤ (𝑛 + 1)^2 / 4. ( 𝜒(𝐺) - the chromatic number of the graph, 𝜒(𝐺̅) - the chromatic number of the complement graph, n - the number of vertices).
Thank you in advance, have a lovely day!

[marcorossettini]

Hi, I'm from Italy and your videos about discrete mathematics are very helpful, thank you!

[satchitnagpal]

Can you also give explanation for how to prove that a graph cannot be colored with less that k colors?

[jingyiwang]

Thank you so much for this wonderful explanation! Graph coloring appears vague to me in lectures. Thanks to your explanation, I have a much clear idea of it and better prepare for my coming discrete mathematics final exam! 🙂

[sanjosekassiels.]

Thank u so much! I finished my activity in 3 min after watching your vid. U the best

[Bk_official]

Thanks a lot you really explained wonderfully so easy to understand.

[nadred]

Hey shawn, can i ask, what software are you using to do all of this? Is it OBS on a computer, or are you capturing on the ipad itself?

[SHASHANKRUSTAGII]

make a video on WAGNER theorem and line graphs
also show line graph of a cycle is a cycle

[ZeroTwo]

i think, now im ready to my D.math final exam, ty!

[HamsaShehadeh]

how about the point that dont connect to any other point? what should i color it? a different color that no point got it? or same as any point color?

[vonage_sasb]

Hello,
Do any one know answer for "Does there exist a 3-edge colourable graph with 10 vertices and 20 edges ?"

[davideperrone]

hi everybody, is there a video about interval graphs?

[gift_tube]

Do lecture on how to calculate the chromatic number for a graph

[meganreader]

Please could you do a video on how to do this?
For each positive integer n prove by induction that a graph G of chromatic number n contains Kn as a subgraph

[aishwaryar]

Could you please do a video on what is math and what are the things we can do with the help of math?

[لُطف-بخ]

Hello, how many chromatic number of (c7) power 2 ????

[steve]

Does someone know the outro song of this video? The musician is called vallow but i can not find the song...

[soveatinkuntur]

can you please make a video about list coloring