filmov
tv
Exponential equation [5^(2x+3)=3125]

Показать описание
An exponential equation is solved [5^(2x+3)=3125]
#algebra #exponentialequation
#algebra #exponentialequation
Exponential equation [5^(2x+3)=3125]
Solve the exponential questions 5^ 2x + 3 =3125 exponential questions #viralvideo
Write the logarithmic equation as an exponential equation. \log_{5} 3125=5 | Plainmath
Solve the exponential equation #equation #maths #mathshorts #mathstricks #olympiad
Solve 3125=(-1-18p)^(5/3)
solve(2/5)^(2x-2)=32/3125. #mathscbse #mathstricks #mathshorts #solve #numbersystem #mathswithaarna
Step-by-Step Tutorial : Solving the Equation 5^(2𝑥−1)=125
IF (3125)^x = x^(-1) Then Find The Value of 'X' | Math Olympiad Preparation
How to find the value of X, given that 125^X = 3125
MTH 161 Solving Exponential Equations Using the One to One Property
How to Write the Exponential Equation 2^5 = 32 in Logarithmic Form
find the value of log5 (log5 3125) :
🤣Modi ji ne to math ki esi taisi kar diye🤣🙆🏻♂️ #shorts #youtubeshorts #viral
E2 Exponential Linear Equations With Change of Base
Q10 p 510 Nelson Solve Exponential Equations Review MHF42
Solving Exponential Equations: Finding the Values of x and y
Grade 8 Algebraic Equations: Lesson 5 - Equations with Exponents
5^(x+1)=26-5^(1-x)
A nice Math Olympiad Simplification | Simplify Exponential Expression | You Should know this Trick
Convert an equation to exponential form to solve
Exponents And Powers Question | Solve For X if (125)^2x=(√5)^3 | Maths Short Tricks | Maths Module
4.4 Solving Exponential Equations Using the One-to-One Property
Solving Exponential Equations by Rewriting One Side of the Equation
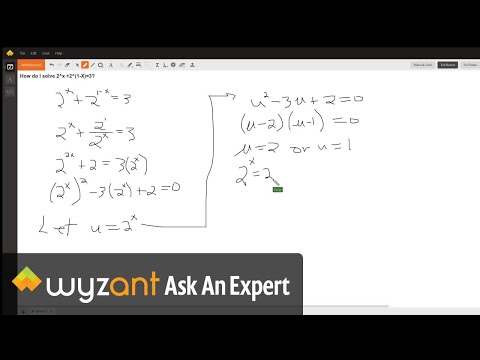
Solve exponential equation that is quadratic in 2^x
Комментарии
![Exponential equation [5^(2x+3)=3125]](https://i.ytimg.com/vi/3YDtaFcxbs4/hqdefault.jpg) 0:01:00
0:01:00
 0:04:19
0:04:19
 0:00:39
0:00:39
 0:00:58
0:00:58
 0:02:18
0:02:18
 0:00:39
0:00:39
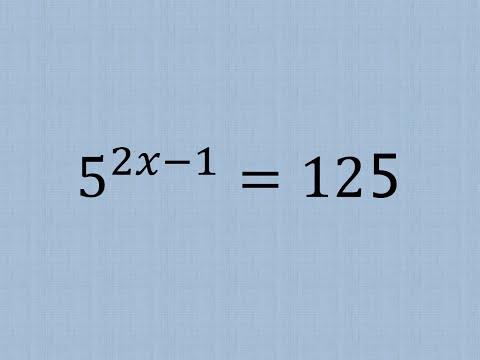 0:01:01
0:01:01
 0:02:03
0:02:03
 0:02:59
0:02:59
 0:18:33
0:18:33
 0:00:23
0:00:23
 0:05:15
0:05:15
 0:00:24
0:00:24
 0:04:24
0:04:24
 0:07:29
0:07:29
 0:09:15
0:09:15
 0:48:35
0:48:35
 0:06:04
0:06:04
 0:13:44
0:13:44
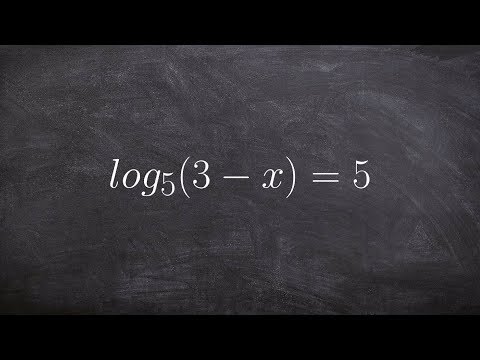 0:01:34
0:01:34
 0:03:02
0:03:02
 0:18:31
0:18:31
 0:09:52
0:09:52
 0:02:56
0:02:56