3.1. Sum of Vectors. Geometry of 2D vectors sum - Linear Algebra and Analytic Geometry

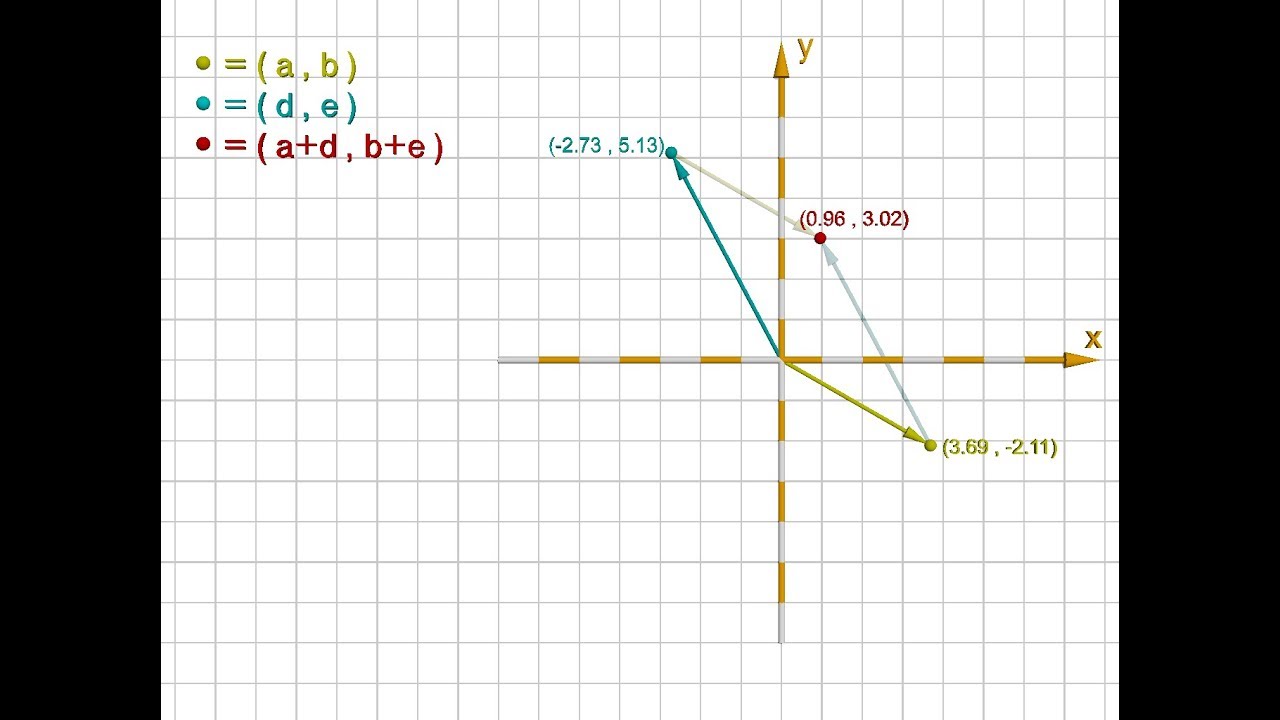
Vectors and points are strictly related: the former are elements of a vector space, the latter are elements of an Euclidean space. In the case the vector space is R^n, vectors correspond to points and viceversa, via the constructions highlighted by the animations in the chapter 2. To visualize the geometrical representation of the structures of sum and multiplication by scalars under such a correspondence, auxiliary drawings, such as arrows, are helpful.
Emphasizing that vectors are
drawn as points and not arrows is never enough. Occasionally, arrows may be useful in making geometrical sense of concept like "angle" between vectors or representing the sum of vectors in R^n.

Course chapters:

0. Introduction

1. Vector Spaces

2. Geometrical interpretation: vectors (algebra)----points (geometry)

3. Geometrical interpretation: sum and product by scalars

4. Sub-Vector Spaces and Linear Combinations

5. Linear Dependence

6. ....