filmov
tv
Multivariable calculus, class #19: Changing the order of integration for double integrals
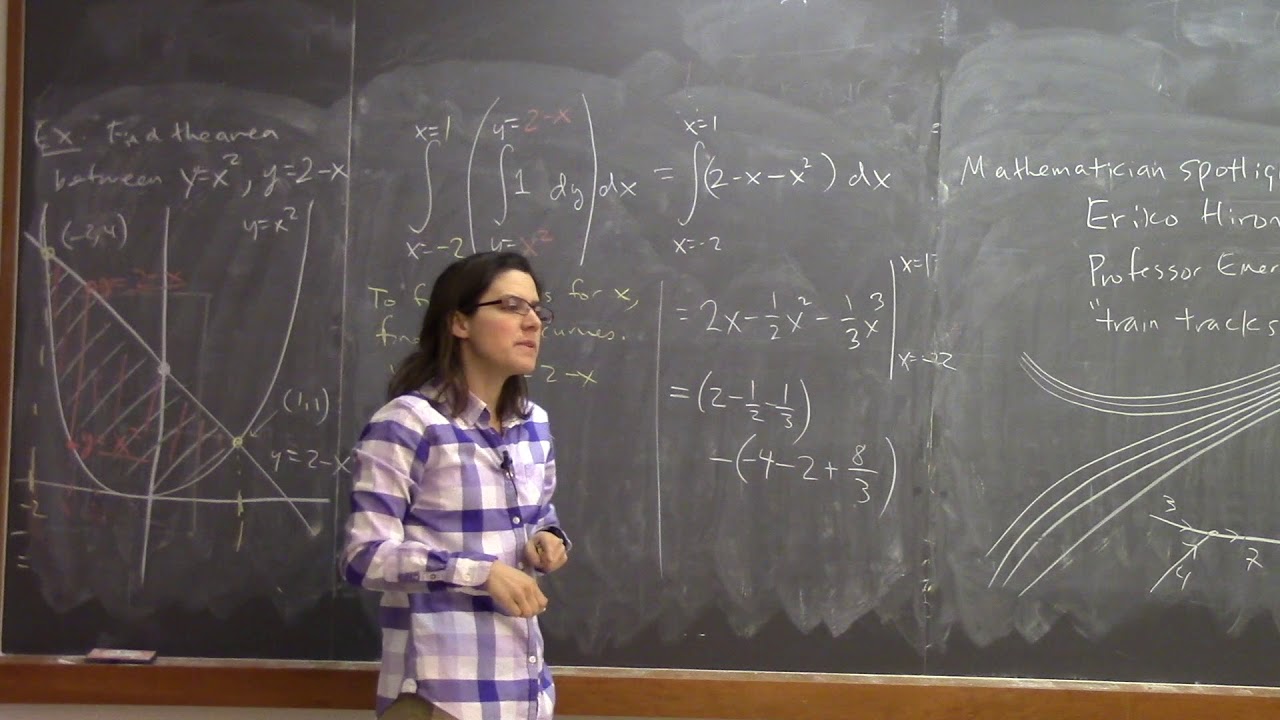
Показать описание
Mathematician spotlight: Eriko Hironaka
We briefly discuss the mathematical notion of "train tracks." We use a double integral to find the area between a line and a parabola, and write it down in both orders of integration. We use double integrals to compute a probability related to two events (me checking out at the store before you). We do two examples of impossible double integrals that become possible when we change the order of integration, because the particular region we are integrating over gives us the needed "derivative of the inside" that we need in order to find an antiderivative for our function. We draw a region where vertical sections would require two different integrals, but horizontal sections only require one. We recommend to go outside and play in the snow.
We briefly discuss the mathematical notion of "train tracks." We use a double integral to find the area between a line and a parabola, and write it down in both orders of integration. We use double integrals to compute a probability related to two events (me checking out at the store before you). We do two examples of impossible double integrals that become possible when we change the order of integration, because the particular region we are integrating over gives us the needed "derivative of the inside" that we need in order to find an antiderivative for our function. We draw a region where vertical sections would require two different integrals, but horizontal sections only require one. We recommend to go outside and play in the snow.
0:48:18
Multivariable calculus, class #19: Changing the order of integration for double integrals
0:12:19
Multivariable Calculus | Changing the order of integration.
0:48:49
Multivariate Calculus: Lecture 19: partial derivatives
0:17:40
Calculus IV - 19 - Changing Order of Integration (2 Variables), Average Value
0:29:14
Multivariable Calculus 2.8.1 - Change of Variables
3:36:30
Multivariable Calculus full Course || Multivariate Calculus Mathematics
0:09:55
Multivariable calculus 3.5.1: Change of variables in single variable calculus
0:10:36
Multivariable Calculus (Part 19)
1:34:05
Multivariate Calculus (Lecture 19): The Total Derivative
0:22:25
Multivariable Calculus Unit 19: Vector fields
0:01:44
Difference Between Partial and Total Derivative
0:08:40
Changing order of integration
0:22:48
Multivariable Calculus | Changing the order of integration in double integrals.
0:06:23
17: Changing Order of Integration - Valuable Vector Calculus
0:00:20
Ducky first meeting with his wife aroob jatoi#makhan
0:59:51
Multivariate Calculus: Lecture 37 Part 1 integration variable change
0:50:18
Multivariable calculus, class #20: Introduction to triple integrals
0:47:58
Multivariable Calculus, Class #25, Gradient Vectors in Polar Coords, Optimization
0:00:20
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
1:17:38
Multivariable Calculus, Lecture #19
0:08:05
Multivariable calculus 3.3.3: Changing the order of integration in triple integrals
1:00:33
Partial Derivatives - Multivariable Calculus
0:04:52
19: Vector Fields - Valuable Vector Calculus
0:08:25
Needham Multivariable Calculus: Maximizing the Directional Derivative
Комментарии