filmov
tv
ODE Exercise #5 - FIrst time, non-homo :v
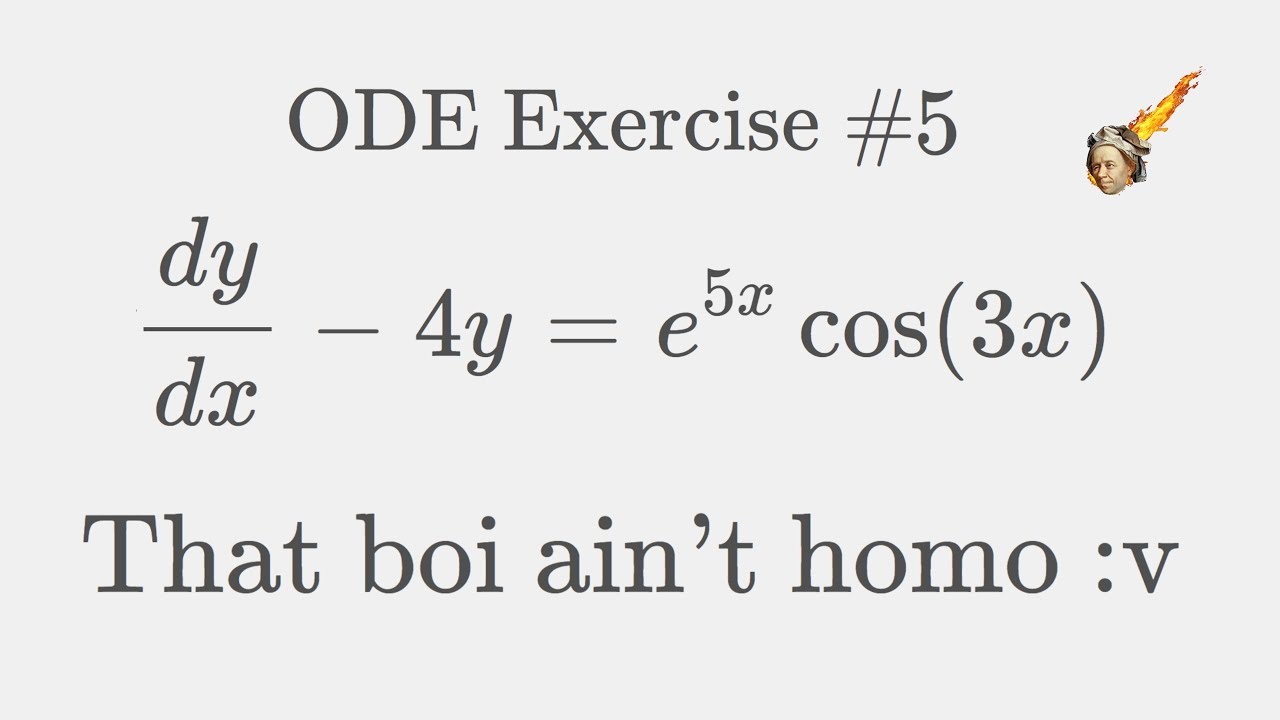
Показать описание
Help me create more free content! =)
In today's episode we are going to deal with a non-homogeneous first order ordinary differential equation for the very first time! :) We are just going to apply what we have learned abstractly before to deal with this boi :3
Visit my website! =)
ODE Exercise #5 - FIrst time, non-homo :v
Exercise 5: Time response of a first order system under different initial conditions
First Order Differential Equation (Exercise Problems) - Part - 5
02.02 First Order Linear Differential Equation - Problem Solution - Example - Exercise - Sample ODE
Numerical Differentiation: First Derivative using Taylor's Series (Exercise 5 - Q1)
Calculus/, first order linear Differential equations exercise 9.2
[Part 2] Differential Equations in 20 more minutes
#2||Linear Differential equation of first order(EXERCISE)||ODE||maths for graduates
VIVID PURPLE 2025 Nike Zoom Vomero 5 | FIRST LOOK + PRICE
Y''=x^2 ...ODE (linear equation of the first order)solved exercise problem from Earl A Cod...
#4||Linear Differential equation of first order(EXERCISE)||ODE||maths for graduates
partial differential equations of first order ( exercise:-1) paper:-3 (semester 5)
first ODE Exercise 15.3
Y'=e^3x +sinx (linear equation of the first order)solved exercise problem from Earl A Coddingto...
Exercise 2.6 Example 5 Equation of first order but not first degree of B.A B.Sc
(semester:- 5) partial differential equations of first order ( Exercise:- 1) (question:-17)
Exercise 5: Solution And First Solver | Python Tutorials For Absolute Beginners In Hindi #37
Ordinary Differential Equation first chapter problem exercise-1.3,1.5 like and subscribe
First Order Differential Equation (Exercise Problems) -;Part - 7
Exercise 2.5 Example 1&2||Equation of first order but not first degree|| #reducebleclairautequat...
Exercise - first degree equations
Lecture 7 - Equation solvable for p || Exercise 2.1 || eq of first order ,not of first degree #ODE
exercise 15.1... first order D.E.. | alpha c Chiang | mathematical economics...
First order and first degree differential equation class12 exercise 11 part A
Комментарии
 0:09:13
0:09:13
 0:09:30
0:09:30
 0:03:13
0:03:13
 0:11:15
0:11:15
 0:13:50
0:13:50
 0:05:28
0:05:28
![[Part 2] Differential](https://i.ytimg.com/vi/ssZlzJgAb_E/hqdefault.jpg) 0:21:42
0:21:42
 0:13:16
0:13:16
 0:01:01
0:01:01
 0:03:20
0:03:20
 0:37:16
0:37:16
 0:05:03
0:05:03
 0:12:25
0:12:25
 0:02:51
0:02:51
 0:25:42
0:25:42
 0:04:53
0:04:53
 0:15:45
0:15:45
 0:05:13
0:05:13
 0:05:26
0:05:26
 0:17:45
0:17:45
 0:05:01
0:05:01
 0:30:36
0:30:36
 0:40:22
0:40:22
 0:18:01
0:18:01