filmov
tv
Calculus 2, Lec 29A, Taylor Series for ln(x) about x = 1, Error Bounds, Series for sin(x)

Показать описание
Calculus 2, Lecture 29A.
(0:00) Lecture plans.
(0:20) Example 1: Taylor series for f(x) = ln(x) centered at a = 1 by using the derivatives' values at 1.
(7:07) Example 2: Find the same Taylor series by integrating 1/x after representing 1/x in a Taylor series centered at a = 1 and the find the interval of convergence.
(14:13) Graphically estimate the error in using the 3rd degree Taylor polynomial for ln(x) centered at a = 1 over the interval from 0.1 to 1.9.
(21:36) Lagrange error bound statement and application over the interval [0.1,1.9] to f(x) = ln(x) and its Taylor series of degree 3 centered at a = 3 (actual error is much smaller).
(29:55) Example 3: apply the Lagrange error bound to the sine function to conclude that the Taylor series for the sine function actually equals it for all x.
(0:00) Lecture plans.
(0:20) Example 1: Taylor series for f(x) = ln(x) centered at a = 1 by using the derivatives' values at 1.
(7:07) Example 2: Find the same Taylor series by integrating 1/x after representing 1/x in a Taylor series centered at a = 1 and the find the interval of convergence.
(14:13) Graphically estimate the error in using the 3rd degree Taylor polynomial for ln(x) centered at a = 1 over the interval from 0.1 to 1.9.
(21:36) Lagrange error bound statement and application over the interval [0.1,1.9] to f(x) = ln(x) and its Taylor series of degree 3 centered at a = 3 (actual error is much smaller).
(29:55) Example 3: apply the Lagrange error bound to the sine function to conclude that the Taylor series for the sine function actually equals it for all x.
 0:34:26
0:34:26
 0:33:02
0:33:02
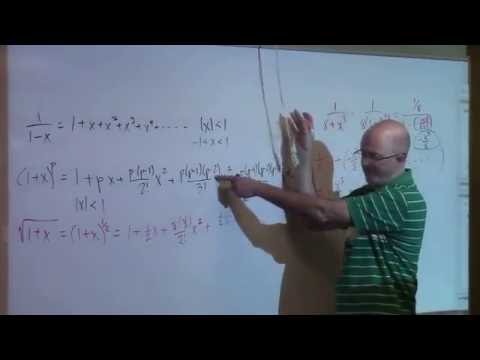 0:19:30
0:19:30
 0:35:59
0:35:59
 0:33:22
0:33:22
 0:35:39
0:35:39
 0:20:25
0:20:25
 0:35:34
0:35:34
 0:13:04
0:13:04
 0:06:34
0:06:34
 0:32:05
0:32:05
 0:01:25
0:01:25
 0:28:08
0:28:08
 0:18:58
0:18:58
 0:30:52
0:30:52
 0:33:54
0:33:54
 0:10:39
0:10:39
 0:33:30
0:33:30
 0:34:29
0:34:29
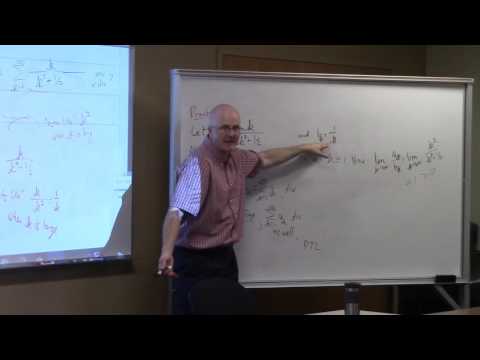 0:24:30
0:24:30
 0:08:03
0:08:03
 0:35:45
0:35:45
 0:29:05
0:29:05
 0:48:20
0:48:20