filmov
tv
dart board probability.
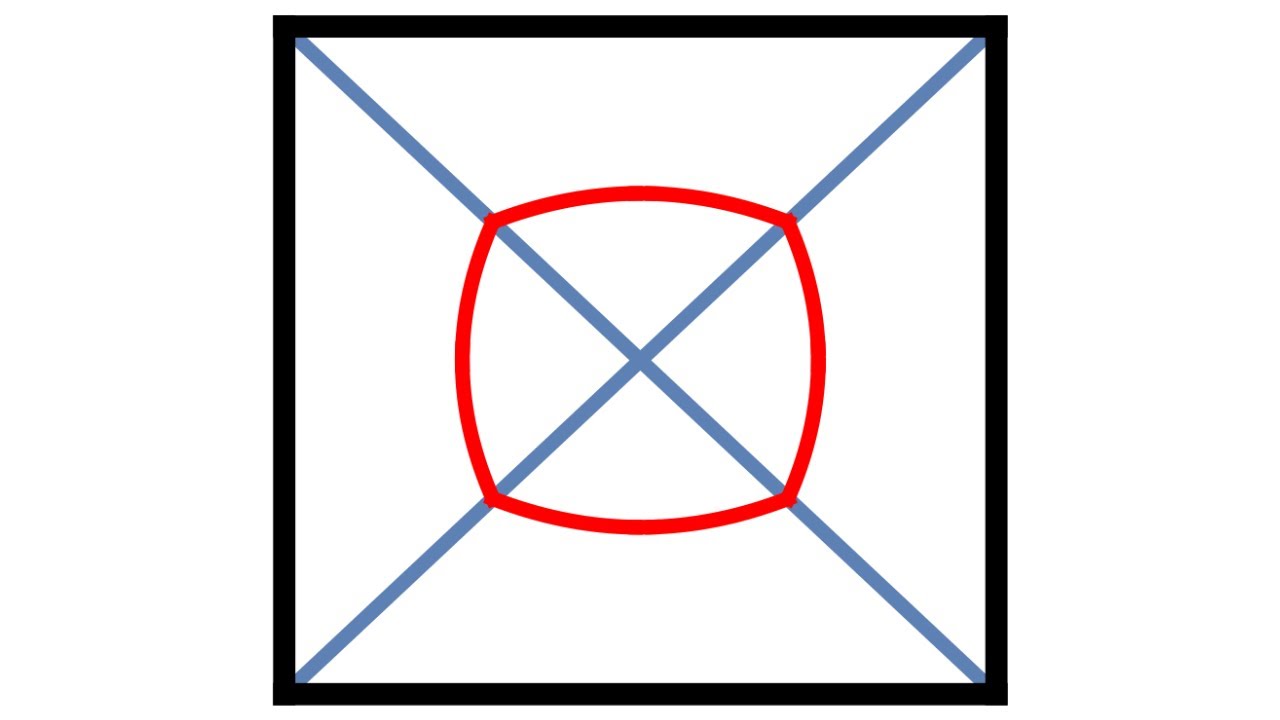
Показать описание
We solve a probability problem involving a square dart board using first semester calculus techniques.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
Probability of Dart hitting blue board??
Probability/Area Problem (Example 2: The Dartboard)
Dartboard Probability Example 1 - - - - MTH-3052
Dartboard Probability Example 3 - - - - MTH-3052
dart board probability.
Find Probability of Dart hitting the blue board.
Making sense of the Dartboard Paradox
Probability tree Dart Board
Dartboard Probability Example 2 - - - - MTH-3052
Class 10th A square Dartboard has sections numbered from 1 to 12 as shown below. Players have
Probability to Win in Dartboard
3 01 3 Experimental Probability dartboard simulation
Darts in Higher Dimensions (with 3blue1brown) - Numberphile
Why “probability of 0” does not mean “impossible” | Probabilities of probabilities, part 2
PROBLEM 18 A dart thrower 'randomly' throws darts at a dartboard If the probability that t...
Probability tree Dart Board
Calculate AND and OR probabilities on a dart board (Probability #6)
Geometry: dartboard probability!
Probability #12 (ex. 10 - a dart throwing problem.)
Simple Probability Tutorial
Section 114 video 10 Dart Board Problem
RHINO - Video 4.05 - What is the probability of hitting a point on a dart board?
90% win rate roulette strategy! You only need to miss 4 numbers and that’s it
Given probability distribution for random variable find probability that dart doesn’t hit board
Комментарии
 0:01:05
0:01:05
 0:09:08
0:09:08
 0:05:33
0:05:33
 0:03:09
0:03:09
 0:07:46
0:07:46
 0:00:59
0:00:59
 0:07:41
0:07:41
 0:06:35
0:06:35
 0:04:40
0:04:40
 0:11:52
0:11:52
 0:05:50
0:05:50
 0:05:57
0:05:57
 0:32:11
0:32:11
 0:10:01
0:10:01
 0:04:10
0:04:10
 0:06:35
0:06:35
 0:02:50
0:02:50
 0:13:25
0:13:25
 0:08:08
0:08:08
 0:14:30
0:14:30
 0:09:43
0:09:43
 0:05:41
0:05:41
 0:00:50
0:00:50
 0:03:35
0:03:35