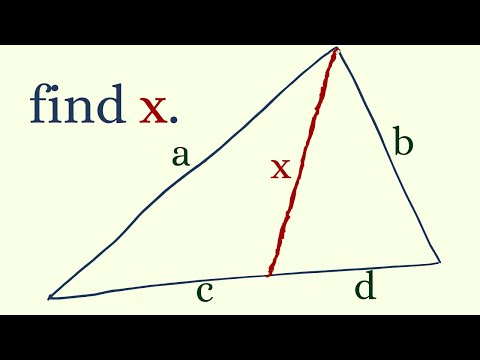
A Viewer Suggested Geometry Puzzle

This video has been suggested by one of my viewers, Qermaq.
To see the comment and the alternative solution, go to:
If you need to post a picture of your solution or idea:
#GeometryPuzzles

EXPLORE:

[timc]

...interesting to see different approaches. Another simple one: draw lines from centre of circle to 60 degree vertex and to tangent point on vertical to form Isosc. triangle with angles = 45 degrees and hypotenuse = sqrt(2); then 'a = sqrt(2)[sin (15)],
so ' b^2 = 1 - 2[(sin (15))^2] = cos(30)', and '2b = 2[sqrt{cos(30)}]'.

[kurtlichtenstein]

This was a fun one!
Speaking of root 3 minus 1 over 2, how about a 3D geometry puzzle: What's the radius of a cylinder of height 1that's inscribed 3D diagonally and symmetrically within a unit cube?

[Qermaq]

Thanks, SyberMath; I was lucky to stumble across this elegant problem. Here's a synopsis of my approach (I need to leave stuff out, space, but comment if you want).

The circle is centered at (1, 1) so it's (x-1)^2+(y-1)^2=1. The slant of the hypotenuse of a 30-60-90 triangle with y-intercept = 2 is y=2-(x/root3).

If we set the ys equal we eventually get x=(3+sqrt(3) +- 4throot(108))/4.

(4throot(108) is root(6*root(3)).)

Both these x values are needed as they are for each of the two points. We need to find the ys to match.

Substitute this in to the original equation as x to find y=2-(x/root3)=(7root(3)-3 +- 4throot(108))/(4root3).

The chord length is the root of the sum of the squares of the differences of the dimensional values; for x, 4throot(27/4) and for y, 4throot(3/4).

So the chord length = = root2 * 4throot3.

This took our buddy about 12 minutes here, subtracting intro and such. Me, it took 12 hours perhaps, and over a half hour to type this. But it was FUN. That's what matters.

[srijanbhowmick]

Really good puzzle ! Loved it ! And thanks to @Qermaq, the original poster of this problem in comments section !

Yayy!!! Solved correctly using a much simpler method, which uses a known theorem....

If A is a point outside a circle, a tangent drawn from A to the circle touches the circle at B, and another straight line from A interests the circle in two points C and D, forming chord CD, then
AB*AB = AC*AD

[BCS-IshtiyakAhmadKhan]

Easy one. Just take centre of circle as (1, 1) and 2 sides of triangle are on axes. Now you can easily find equation of hypotenuse. Now calculate perpendicular distance from (1, 1) to the line(hypotenuse).after that you can easily find chord length

[klementhajrullaj]

From a sphere with radius r is derived the largest regular triangular pyramid. What are its dimensions? Thank you! ...

[michaelsadovsky]

A very nice task, however, the solution is heavily incomplete. You have voluntarily assigned the shorter leg of the rectangular triangle to be equal to 2 (just check the written formulation of the problem!). You must consider two more cases: the former is when the longer leg is equal to 2, and the latter is when the height erected from the right corner is equal to 2. Surprisingly, all three cases have the solution, each. And the answers are different; thus, the problem has three answers what makes it even more interesting! :)

[AsfuNtendstoINFINITY]

Thanks for the nice problem, SyberMath :)

[beautifulmindinpuzzles]

Alternate Solution( much shorter):
The area of the triangle is 2SQRT3. Connect the center of the circle to the vertices of the triangle. Three other triangles are formed. The sum of the areas of these three triangles is equal to the area of the original triangle. Find a, then find b.

[srijanbhowmick]

Can I post a problem on divisors ? Which has the potential to make it into one of your videos ?

[tonyhaddad]

My way was by getting the erea of the 30-90-60 triangle by two methode to get the perpendicular to the cord and after that were done !!(by pythagorean theorem )

[shamilbabayev]

height is 2, but which height of the triangle?

[diogenissiganos]

I solved it using coordinate geometry and it was really satisfying!