filmov
tv
Learn to Differentiate ln(x²) in 40 seconds

Показать описание
Want to learn how to differentiate ln(x²) quickly? This 40-second tutorial explains the process using only the chain rule. No complicated formulas or unnecessary steps. By the end, you'll be able to confidently tackle similar derivative problems.
--------------------------------------------------------------------------------------------------------------------------------------------------------
Finding the Derivative of ln(x³):
ln(x³) ⟹power rule for logs⟹3ln(x) ⟹ differentiate⟹d/dx(ln(x³)) = 3d/dx(ln(x)) = 3/x (answer)
------------------------------------------------------------------------------------------------------------------------------------------------------
d/dx ln(x⁴)
= d/dx (4 ln(x)) bring 4 down
= 4 * d/dx ln(x) differentiate
= 4 * 1/x
=4/x answer
-------------------------------------------------------------------------------------------------------------------------------------------------------
Step into our world of high-quality merchandise, where every piece is crafted to make you feel something special. Our clothing and accessories are designed to make you feel confident, stylish, and comfortable, so you can show off your unique personality and values. And when you wear our products, you're not just showing your support for our brand - you're joining a community of like-minded individuals who share your passion and values. Each purchase is an experience that connects you with our mission and shows the world what you stand for. Thank you for considering our merchandise - we hope that our products will bring you joy, inspiration, and a sense of belonging. Together, we can make a difference.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
--------------------------------------------------------------------------------------------------------------------------------------------------------------
Imagine feeling confident and empowered in calculus class, tackling even the toughest problems with ease. With 3000 Solved Problems in Calculus by Schaum's, that dream can become a reality. Click on the link now and take the first step towards unlocking your full potential in calculus - you won't regret it.
--------------------------------------------------------------------------------------------------------------------------------------------------------------
The rules of logarithms have a long history dating back to the 16th century with John Napier's introduction of the concept of logarithms. In the 17th century, John Wallis further developed logarithmic differentiation. Logarithms were then used extensively in scientific and engineering fields in the 18th and 19th centuries. Today, logarithms are widely used in a variety of fields, including finance, physics, chemistry, and engineering, with the rules of logarithms playing a crucial role in simplifying and solving complex equations.
The history of logarithms demonstrates how mathematical concepts can evolve over time and remain relevant to modern-day applications. Logarithms were replaced by electronic calculators in the early 20th century but remain an important tool in mathematics and other fields. Overall, logarithms have proven to be a useful tool for handling large numbers and complicated equations and are a testament to the ongoing development and evolution of mathematical concepts.
--------------------------------------------------------------------------------------------------------------------------------------------------------
Finding the Derivative of ln(x³):
ln(x³) ⟹power rule for logs⟹3ln(x) ⟹ differentiate⟹d/dx(ln(x³)) = 3d/dx(ln(x)) = 3/x (answer)
------------------------------------------------------------------------------------------------------------------------------------------------------
d/dx ln(x⁴)
= d/dx (4 ln(x)) bring 4 down
= 4 * d/dx ln(x) differentiate
= 4 * 1/x
=4/x answer
-------------------------------------------------------------------------------------------------------------------------------------------------------
Step into our world of high-quality merchandise, where every piece is crafted to make you feel something special. Our clothing and accessories are designed to make you feel confident, stylish, and comfortable, so you can show off your unique personality and values. And when you wear our products, you're not just showing your support for our brand - you're joining a community of like-minded individuals who share your passion and values. Each purchase is an experience that connects you with our mission and shows the world what you stand for. Thank you for considering our merchandise - we hope that our products will bring you joy, inspiration, and a sense of belonging. Together, we can make a difference.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
--------------------------------------------------------------------------------------------------------------------------------------------------------------
Imagine feeling confident and empowered in calculus class, tackling even the toughest problems with ease. With 3000 Solved Problems in Calculus by Schaum's, that dream can become a reality. Click on the link now and take the first step towards unlocking your full potential in calculus - you won't regret it.
--------------------------------------------------------------------------------------------------------------------------------------------------------------
The rules of logarithms have a long history dating back to the 16th century with John Napier's introduction of the concept of logarithms. In the 17th century, John Wallis further developed logarithmic differentiation. Logarithms were then used extensively in scientific and engineering fields in the 18th and 19th centuries. Today, logarithms are widely used in a variety of fields, including finance, physics, chemistry, and engineering, with the rules of logarithms playing a crucial role in simplifying and solving complex equations.
The history of logarithms demonstrates how mathematical concepts can evolve over time and remain relevant to modern-day applications. Logarithms were replaced by electronic calculators in the early 20th century but remain an important tool in mathematics and other fields. Overall, logarithms have proven to be a useful tool for handling large numbers and complicated equations and are a testament to the ongoing development and evolution of mathematical concepts.
Комментарии
 0:00:39
0:00:39
 0:01:04
0:01:04
 0:00:43
0:00:43
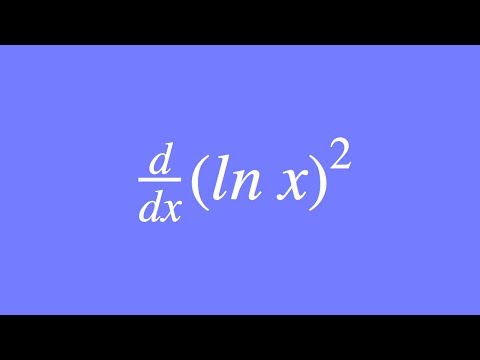 0:01:55
0:01:55
 0:01:44
0:01:44
 0:01:36
0:01:36
 0:02:30
0:02:30
 0:02:47
0:02:47
 0:00:42
0:00:42
 0:00:29
0:00:29
 0:02:47
0:02:47
 0:01:40
0:01:40
 0:03:15
0:03:15
 0:01:02
0:01:02
 0:01:33
0:01:33
 0:00:50
0:00:50
 0:03:28
0:03:28
 0:00:54
0:00:54
 0:06:45
0:06:45
 0:01:53
0:01:53
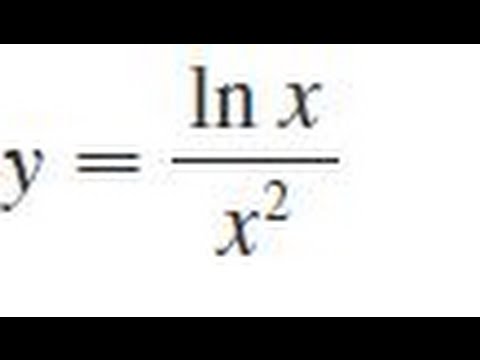 0:02:11
0:02:11
 0:01:59
0:01:59
 0:00:29
0:00:29
 0:00:41
0:00:41