Binary, Hanoi and Sierpinski, part 1

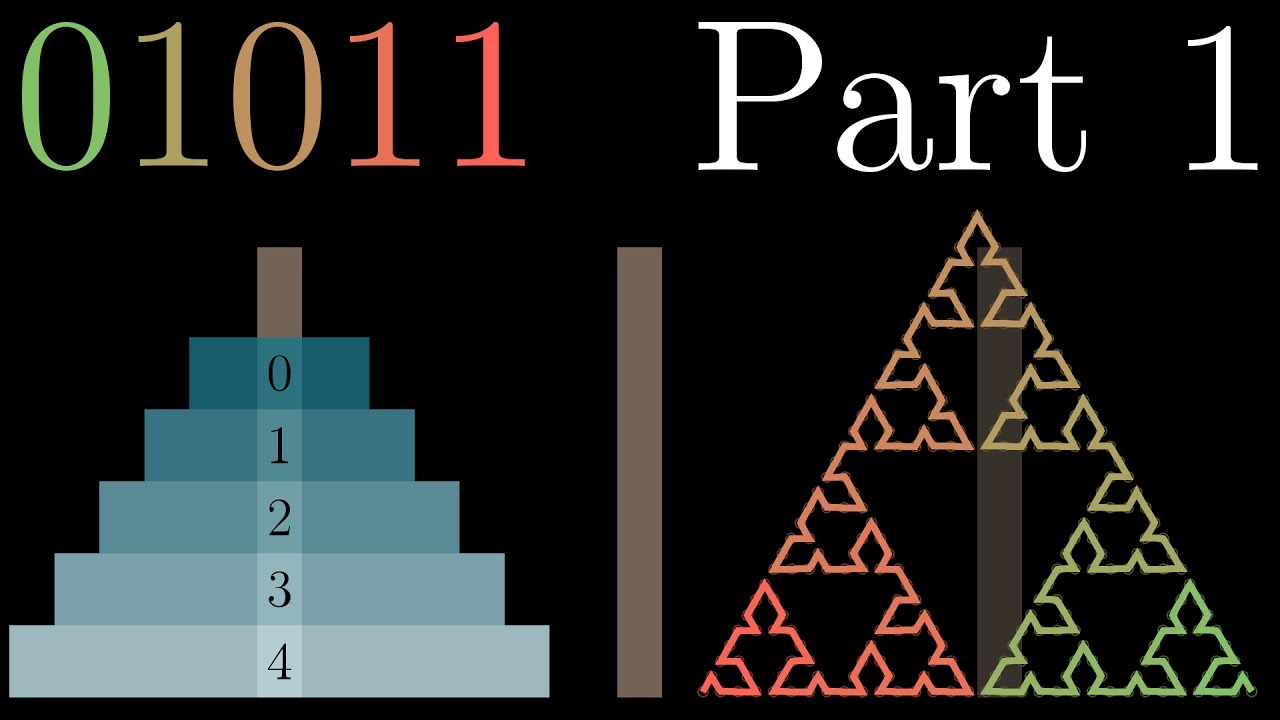
Binary counting can solve the towers of Hanoi puzzle, and if this isn't surprising enough, it can lead to a method for finding a curve that fills Sierpinski's triangle (which I get to in part 2).

I also want to give a special shoutout to the following patrons: CrypticSwarm, Ali Yahya, Dave Nicponski, Juan Batiz-Benet, Yu Jun, Othman Alikhan, Markus Persson, Joseph John Cox, Luc Ritchie, Einar Wikheim Johansen, Rish Kundalia, Achille Brighton, Kirk Werklund, Ripta Pasay, Felipe Diniz, Chris, Curtis Mitchell, Ari Royce, Bright , Myles Buckley, Robert P Zuckett, Andy Petsch, Otavio good, Karthik T, Steve Muench, Viesulas Sliupas, Steffen Persch, Brendan Shah, Andrew Mcnab, Matt Parlmer, Naoki Orai, Dan Davison, Jose Oscar Mur-Miranda, Aidan Boneham, Brent Kennedy, Henry Reich, Sean Bibby, Paul Constantine, Justin Clark, Mohannad Elhamod, Denis, Ben Granger, Jeffrey Herman, Jacob Young.

[TheGerogero]

How is this the first time I hear that _bit_ is short for _binary digit_...

Mind blown.

[enotirab]

I am software developer (who also has a love for math) and it never once occurred to me that counting was a recursive action. I am continuously amazed at how elegant and simple your videos are and how effective they are at showing complex ideas in an approachable way. Thanks for all your hard work!

[ZardoDhieldor]

I simply love your videos! I'm a mathematics student, so I'm used to the joy of understanding, but that doesn't make it any less exciting! And your animations are a wonderful, powerful and beautiful help in this delightful process!
I may be repeating myself but nonetheless: Thank you! Keep up the great work! :)

[EmilMacko]

I've used Desmos for a little over a year now, and I'm sad that my math classes never use it. I mainly just use it for my game development and for math-fun. It's the best math-function graphing tool I've ever used.

[kayleighlehrman]

another great perspective that I just realized...count up how many times each disc /has/ to move, starting from the bottom. disc n has to move just once, disc n-1 has to move twice (once to get off of disc n and once to get back on again), disc n-2 has to move four times, etc

[tomoakhill]

I saw this puzzle 50 years ago in high school. My classmates were struggling with it. I just sat down and did it without hesitation. It has always been obvious to me. I earned a Masters Degree in Computer Science. It seemed to me trivially obvious that this puzzle was binary counting. 3Blue1Brown explains this beautifully.

[zachallen]

Your videos captured my attention so well in your calculus lectures, that I finally dispelled the notion that I was not a math person, and simply needed to try harder. Finally going back to school, and no longer avoiding math intensive fields! Seriously though, this video is so cool, my girlfriend generally isn’t interested in this kind of stuff, but she loved this as well. Thank you, for working hard to put this stuff out.

[Cyanogenoid]

Wouldn't it make more sense for the binary numbers at 6:05 and 11:20 to be coloured exactly the opposite way they are, i.e. leftmost digit bright blue and rightmost digit dark blue? That way the colour of the digit that flips corresponds to the same colour of disk that's actually moved.

[SaveSoilSaveSoil]

"Counting is self-similar" -- fantastic and thought provoking!

[VaraNiN]

A simpler rule (only needing to count in base ten (or not at all when you got into the rythm) I noticed when trying this out:

- On an odd numbered move: Move the 0-piece once to the right (or left, works both ways as long as you dont switch direction)
- On an even numbered move: Move the largest piece you can move (which is never the 0-piece) to the only legal place

Which is, of course the same as counting in binary, but a little simpler to put to use imo :)

[snowfloofcathug]

I never thought about it, I just found it so simple once I found the pattern, but I never could've imagined it'd be hiding something more complex and so beautiful

[nindorox]

This one was incredible! the math was really cool and the animations were insane!

and you're supported by the best graphing calculator ever!!!

[ilonachan]

Wow, just solved a programming task for the Towers of Hanoi, and remembered that this video existed. Thanks for saving the day _and_ blowing my mind.

[yaeldillies]

I always felt like counting in binary when solving towers of Hanoi! That's amazing now that I understand why.

[morgengabe]

Once in year 7 or 8 I was in maths and at the end of the class the teacher asked the class how we could improve our understanding of the content covered in class that day. Some students suggested things like calculating the cost and change (if paid in cash) of grocery expenditure. Another said "counting" and the teacher laughed, and said "counting what?", the student said "anything", the teacher laughed again but louder and with the rest of the class before saying "No [name], I don't think counting is going to help".
Looks like counting is pretty useful right about now.

[dddtl]

I really like your use of the Computer Modern typeface!

[bellac]

I've never even taken a CS class but this is so fascinating! I love seeing videos appreciating the thrilling cohesiveness which seems to appear in every area of mathematics. Absolutely adore these videos, thanks for putting them out there!

[pbeauchene]

So nice ! I taught the Hanoi towers when I was teaching algorithmics, because it was the simplest example I could think of with exponential complexity, but I never knew this trick with binary counting !
There is an error in the transcript at 7:55 : the number of steps required is 2^n - 1, not 2^(n-1).

[MrSilbarita]

Holy! This is absolutely amazing. I solved this puzzle for/with a student of mine and came to these conclusions, but the binary counting perspective is simply mesmerizing. Thank you for this video!

[maximkazhenkov]

Fun trivia: According to legend, when the full 64 disc puzzle is solved, the world will end. Assuming 1 move per second, it would take 2^64-1 = 1.84*10^19 seconds or 585 billion years, which is incidentally the time it takes until the last star in the universe burns out.