filmov
tv
A2 U4.06

Показать описание
A2 U4.06
A2 U4.06
A2 U4
A2 U4 Obj 1-10 hw Solution to #3-6
A2 U4 6-7 Notes Part 2 Ex 1
A2 U4 6-7 Notes Part 3 Ex 2a
A2 U4 6-7 Notes Part 2 Ex 2b
A2 U4 LO1-LO5 Review #5,6
A2 U4 6-7 Notes Part 2 Ex 2a
A2 U4 6-7 Notes Part 3 Page 1
A2 - U4 - Topic 1 Simplify
A2 U4 6-7 Notes Part 3 ex. 2b
A2 - U4 - 4.6 Direct Variation
PC U4.06
BME U4 A2 ANCM
A2 U4 Obj 1-10 hw Solution to #7
A2 U4 Zeros and Multiplicity
Mounting Wireless & Wired Cycling Computers
FisiolPulm U4 A2 Meza Enrique 'Mecánica Respiratoria'
NBTC U4 A2 TEMC
A2 U4.05
A2 U4 Explore the Skill
A2 U4.05
A2 U4 Simplifying Radical Expressions
Комментарии
 0:12:45
0:12:45
 0:05:46
0:05:46
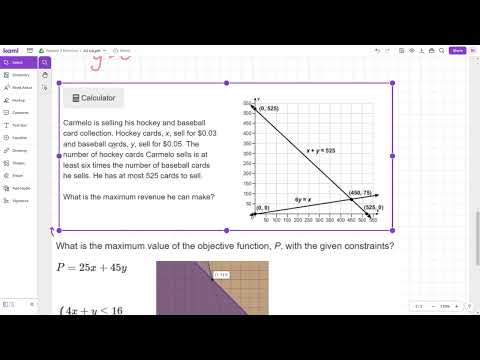 0:14:49
0:14:49
 0:01:33
0:01:33
 0:06:07
0:06:07
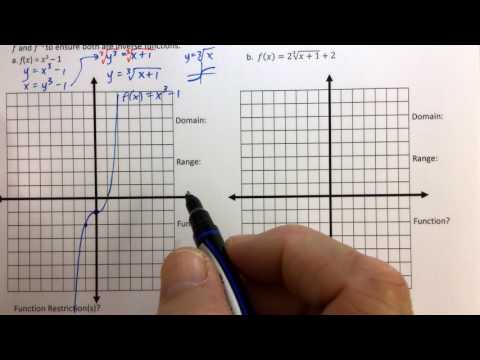 0:06:27
0:06:27
 0:02:56
0:02:56
 0:02:42
0:02:42
 0:07:56
0:07:56
 0:05:35
0:05:35
 0:18:24
0:18:24
 0:04:00
0:04:00
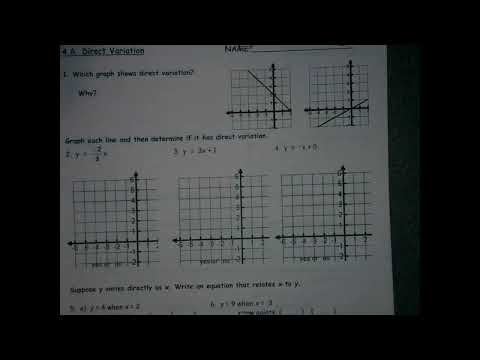 0:24:24
0:24:24
 0:05:55
0:05:55
 0:02:28
0:02:28
 0:03:03
0:03:03
 0:06:41
0:06:41
 0:04:11
0:04:11
 0:06:50
0:06:50
 0:06:36
0:06:36
 0:05:29
0:05:29
 0:02:06
0:02:06
 0:05:25
0:05:25
 0:18:38
0:18:38