filmov
tv
The Christoffel Symbols In Riemannian Geometry

Показать описание
The illustrious Christoffel Symbols are requisite to any study of curved surfaces, but can their abstract nature be made more concrete and physical? Here our exploration of the daunting subject of differential geometry continues, as with a host of vivid and visceral 3D animations we attempt to explore the nature of these mathematical objects, whilst striving to bring the wonderful world of Riemannian Geometry to life!
We highly recommend watching "An Introduction to Curvilinear Coordinates" before viewing this video:
If you're completely new to the subject of the Christoffel Symbols, try starting here:
Lastly, a huge thank you to our Patreon supporters, for continuing to make our channel a feasible endeavor. Especial thanks to the following individuals:
Henry Lindner
Antsu Sausanen
Michael O'Connor
James Bretz
Jordan Rosario
Please consider supporting the channel here:
Video Contents:
00:00 - Introduction
00:50 - Curvilinear Coordinate Recap
02:17 - Basis Vectors & Christoffel Symbols: Physical Intuition
06:49 - Basis Vectors & Christoffel Symbols on a Curved Manifold
13:17 - Extrinsic Solution of a 2-Sphere
14:49 - Metric Tensor & Intrinsic Method
19:15 - Levi-Civita Constraints; Christoffel Equation Derivation & Interpretation
27:04 - Example Problem/Intrinsic Solution of a 2-Sphere
31:20 - Global vs. Local Flatness/Conclusion
We highly recommend watching "An Introduction to Curvilinear Coordinates" before viewing this video:
If you're completely new to the subject of the Christoffel Symbols, try starting here:
Lastly, a huge thank you to our Patreon supporters, for continuing to make our channel a feasible endeavor. Especial thanks to the following individuals:
Henry Lindner
Antsu Sausanen
Michael O'Connor
James Bretz
Jordan Rosario
Please consider supporting the channel here:
Video Contents:
00:00 - Introduction
00:50 - Curvilinear Coordinate Recap
02:17 - Basis Vectors & Christoffel Symbols: Physical Intuition
06:49 - Basis Vectors & Christoffel Symbols on a Curved Manifold
13:17 - Extrinsic Solution of a 2-Sphere
14:49 - Metric Tensor & Intrinsic Method
19:15 - Levi-Civita Constraints; Christoffel Equation Derivation & Interpretation
27:04 - Example Problem/Intrinsic Solution of a 2-Sphere
31:20 - Global vs. Local Flatness/Conclusion
Комментарии
 0:34:01
0:34:01
 0:23:38
0:23:38
 0:00:16
0:00:16
 0:18:05
0:18:05
 0:26:01
0:26:01
 0:13:19
0:13:19
 0:42:50
0:42:50
 0:28:52
0:28:52
 0:17:06
0:17:06
 0:21:40
0:21:40
 0:07:46
0:07:46
 0:10:00
0:10:00
 0:07:26
0:07:26
 0:50:04
0:50:04
![[GR 24/05/2023] 12:](https://i.ytimg.com/vi/whypAdIdJAE/hqdefault.jpg) 0:49:27
0:49:27
 0:01:43
0:01:43
 0:18:03
0:18:03
 0:15:43
0:15:43
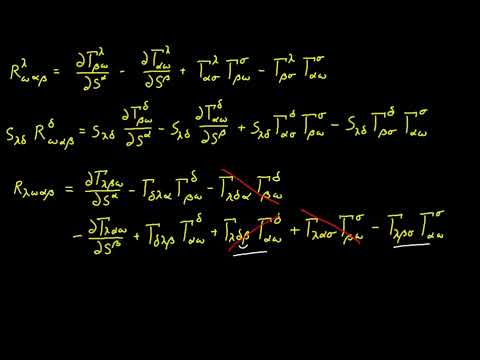 0:21:01
0:21:01
 0:03:06
0:03:06
 0:21:24
0:21:24
 0:14:16
0:14:16
 0:20:44
0:20:44
 0:09:11
0:09:11