filmov
tv
Convert the complex number -sqrt(3) + i in polar form

Показать описание
In this video, we will learn to convert the complex number -sqrt(3) + i in polar form. Here, i is the imaginary unit.
The link given below is of video verifying the identity cos(pi - x) = -cos x
The link given below is of video verifying the identity sin(pi - x) = -sin x
Other topics of this video are:
-sqrt(3) + i
modulus and argument of -sqrt(3) + i
Find the modulus and argument of -sqrt(3) + i
I, Ravi Ranjan Kumar Singh, have produced this video. All credits of this video belong to me.
The link given below is of video verifying the identity cos(pi - x) = -cos x
The link given below is of video verifying the identity sin(pi - x) = -sin x
Other topics of this video are:
-sqrt(3) + i
modulus and argument of -sqrt(3) + i
Find the modulus and argument of -sqrt(3) + i
I, Ravi Ranjan Kumar Singh, have produced this video. All credits of this video belong to me.
Convert the complex number -sqrt(3) + i in polar form
Convert the complex number sqrt(3) + i in polar form
How to Write a Complex Number in Polar Form, Example with 3 + 3i
Convert of the complex number in the polar form: `sqrt(3)+i`...
Convert the complex number `(1+isqrt(3))` into polar form.
Convert the complex number -3 in polar form
Convert the complex number (2 + 6 sqrt(3)i)/(5 + sqrt(3)i) in the polar form
Express the Complex Number -3 + 3i in Polar Form
Complex Numbers In Polar - De Moivre's Theorem
How to write complex numbers in polar form
Convert of the complex number in the polar form: `sqrt(3)+i`...
Converting Complex Number to its Polar Form (Resultant and Angle) using CASIO fx-991ES PLUS Calcu
how to convert complex numbers into polar form | (root 3 - i)^4 /(root 3 + i)^4 and (1+i)^5 /(1-i)^5
Convert the complex number `(-2 + 2i sqrt(3))` into polar form.
Class 12 | Maths | Complex Numbers | Convert the complex number (1+i√3) into polar form.
How to write -2 + 2sq rt 3i complex number in polar form
Complex Number in quadrant 3 to Trigonometric Polar Form Grade 11 NCERT
Convert the complex number `(-16)/(1+i sqrt(3))` into polar form. |Class 11 MATH | Doubtnut
Convert the complex numbers into polar form : \[ \frac{(\sqrt{3}-1)...
(i) Convert `(-16)/(1-isqrt(3))` into polar form. (ii) Convert `(1+7i)/((2-i)^(2))` into polar form.
-1+√3i || Polar Form of a Complex Number
Necessity of complex numbers
Complex Number Division | using Calculator (Casio fx-991MS)
How to find the principal square root of a complex number
Комментарии
 0:04:06
0:04:06
 0:03:01
0:03:01
 0:04:54
0:04:54
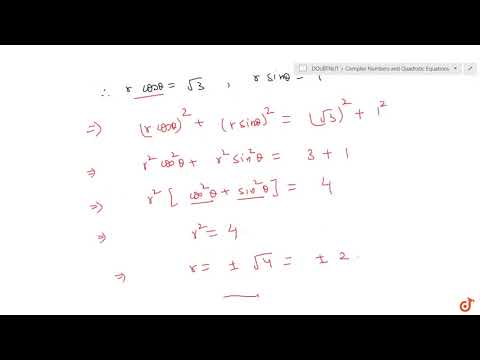 0:04:09
0:04:09
 0:01:57
0:01:57
 0:02:33
0:02:33
 0:04:48
0:04:48
 0:07:05
0:07:05
 1:04:47
1:04:47
 0:07:04
0:07:04
 0:03:32
0:03:32
 0:00:59
0:00:59
 0:17:47
0:17:47
 0:03:18
0:03:18
 0:03:17
0:03:17
 0:06:36
0:06:36
 0:06:49
0:06:49
 0:09:37
0:09:37
 0:05:19
0:05:19
 0:05:33
0:05:33
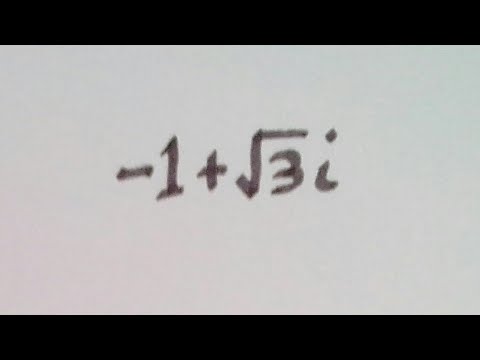 0:03:06
0:03:06
 0:07:39
0:07:39
 0:00:34
0:00:34
 0:00:59
0:00:59