The Bernstein problem for equations of minimal surface type

Speaker: Connor Mooney, University of California, Irvine

2020 Fields Medal Symposium

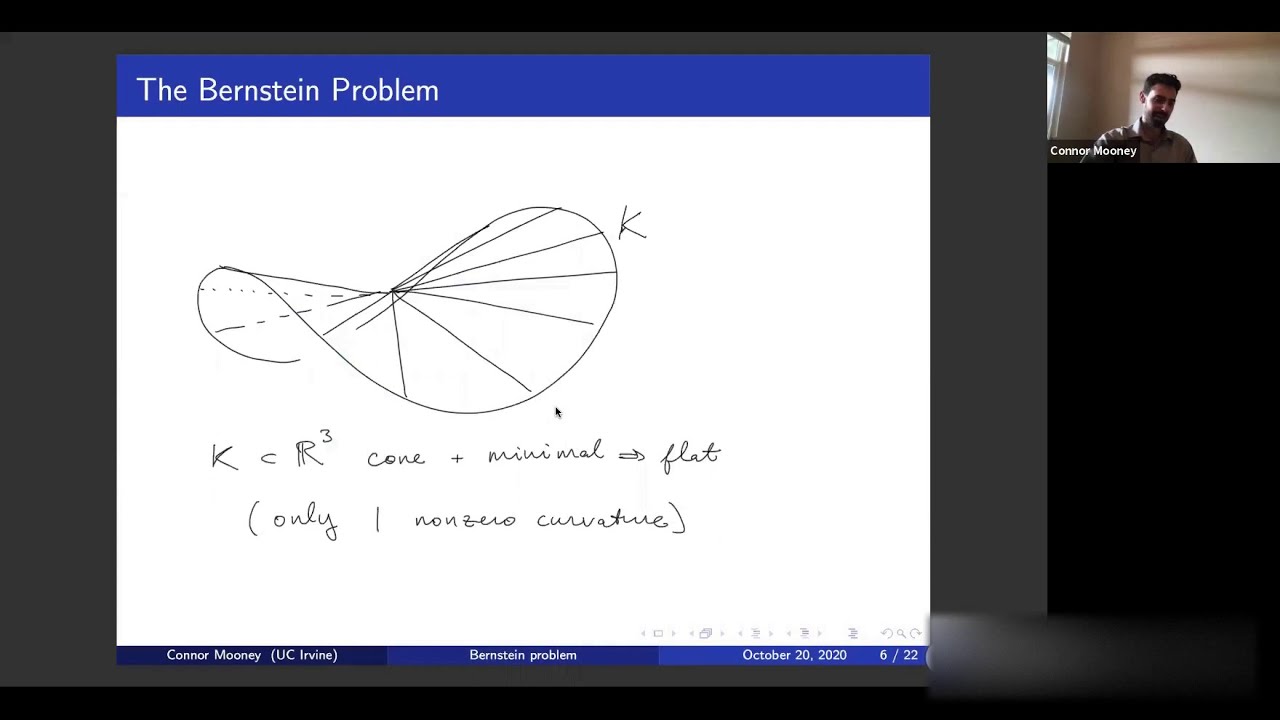
Abstract: The Bernstein problem asks whether entire minimal graphs in dimension N + 1 are necessarily hyperplanes. This problem was solved in combined works of Bernstein, Fleming, De Giorgi, Almgren, and Simons ("yes" if N (less than) 8), and Bombieri-De Giorgi-Giusti ("no" otherwise). We will discuss the analogue of this problem for minimizers of general parametric elliptic functionals. In particular, we will discuss new examples of nonlinear entire graphical minimizers in dimension N = 6, and recent joint work with Y. Yang towards constructing such examples in the lowest possible dimension N = 4.