filmov
tv
Galois group of x^3-3x+3
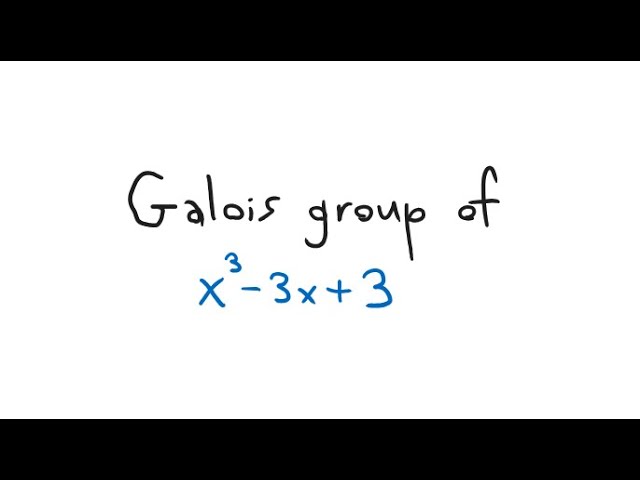
Показать описание
What is the Galois group of x^3-3x+3? EDIT: The method used in this video does not show that the polynomial has only a single real root since we didn't test for where the polynomial is increasing/decreasing. To see why it only has one root in R we can either observe that at both critical points the function is positive (so it can't have a root between these points, since then the derivative would be 0 at some point between -1 and 1), or we could use the first derivative to see where the function is increasing/decreasing.
Galois group of x^3-3x+3
How to find the Galois Group of x^3+3x+3
Galois group of x^3-3x+1
Example of Galois Group degree 3 polynomial
Galois Theory Lecture 18: Galois Group of Irreducible Cubic Polynomials
Galois 8a
Galois Groups of Cubic Polynomials (Algebra 3: Lecture 27 Video 1)
Galois Group of x^4-2
Examples of Galois Extensions: The Splitting Field of x^3-2 (Algebra 3: Lecture 18 Video 2)
Abstract Algebra II: Galois groups of polynomials order 2 and 3, cubic formula, 2-18-22 part 1
MATH 368 Galois Group of a Palindromic Sextic (Part II)
Galois Group of Cubic Polynomial which is Symmetric
Part 11.1.3 Galois Group and examples
Galois group of x^4-4x+2
Galois group of polynomial
Example of Galois group degree 4 polynomial
Galois group of x^4-2x^3-8x-3
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Prove Galois group for R/Q (real number over rational) is a trivial group
But why is there no quintic formula? | Galois Theory
The Insolvability of the Quintic
Order of Galois Groups
COC4010_1.19_Crypto Maths3 _Galois Fields_Modular Polynomial Arithmetic
Abstract Algebra II: Galois group of xxx-2 over Q, 3-27-19
Комментарии
 0:05:35
0:05:35
 0:01:46
0:01:46
 0:04:44
0:04:44
 0:06:47
0:06:47
 0:19:03
0:19:03
 0:16:50
0:16:50
 0:17:49
0:17:49
 0:12:27
0:12:27
 0:20:19
0:20:19
 0:59:51
0:59:51
 0:11:34
0:11:34
 0:20:47
0:20:47
 0:05:26
0:05:26
 0:12:53
0:12:53
 0:13:43
0:13:43
 0:03:26
0:03:26
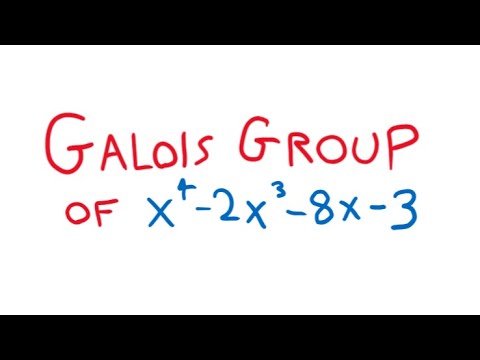 0:08:34
0:08:34
 0:00:38
0:00:38
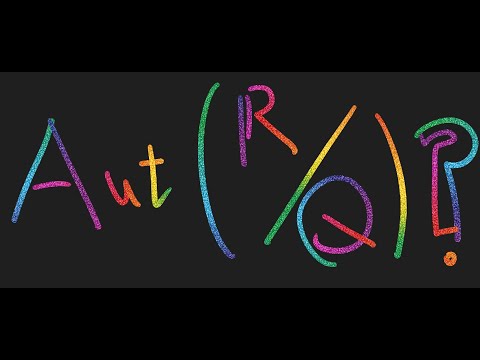 0:05:18
0:05:18
 0:11:59
0:11:59
 0:10:19
0:10:19
 0:21:06
0:21:06
 0:24:11
0:24:11
 0:47:47
0:47:47